
Wetenschap
Wat is de frequentie en golflengte van materiegolf geassocieerd met een 10 elektronen volt vrij zijn?
Inzicht in de concepten
* de Broglie -golflengte: De de Broglie-hypothese stelt dat alle materie golfachtige eigenschappen vertoont. De golflengte van een deeltje is omgekeerd evenredig met zijn momentum:
λ =h / p
waar:
* λ is de de Broglie -golflengte
* H is de constante van Planck (6.63 x 10^-34 JS)
* P is het momentum van het deeltje
* Kinetische energie en momentum: De kinetische energie (KE) van een deeltje is gerelateerd aan zijn momentum:
Ke =p^2 / 2m
waar:
* M is de massa van het deeltje
Berekeningen
1. Converteer elektronenvolt naar joules:
1 eV =1.602 x 10^-19 j
Daarom, 10 eV =10 * 1.602 x 10^-19 j =1.602 x 10^-18 j
2. Bereken het momentum:
Ke =p^2 / 2m
P^2 =2MKE
P =√ (2mke)
* De massa van een elektron (m) is 9.11 x 10^-31 kg.
* Vervang de waarden en bereken p.
3. Bereken de de Broglie -golflengte:
λ =h / p
Vervang de waarden van H en P die u berekende.
4. Bereken de frequentie:
De relatie tussen golflengte (λ), frequentie (f) en de snelheid van het licht (c) is:
C =λf
Omdat het elektron niet-relativistisch is, is de snelheid niet de snelheid van het licht. We moeten de snelheid van het elektron gebruiken.
* Bereken eerst de snelheid (V) van het elektron met behulp van de kinetische energie:
Ke =1/2 * mv^2
v =√ (2Ke / m)
* Bereken vervolgens de frequentie:
f =v / λ
Laten we de berekeningen doen:
1. Momentum (P):
p =√ (2 * 9.11 x 10^-31 kg * 1.602 x 10^-18 j) ≈ 1,92 x 10^-24 kg m/s
2. de Broglie -golflengte (λ):
λ =(6,63 x 10^-34 js) / (1,92 x 10^-24 kg m / s) ≈ 3,46 x 10^-10 m
3. snelheid (V):
v =√ (2 * 1.602 x 10^-18 j / 9.11 x 10^-31 kg) ≈ 1,88 x 10^6 m / s
4. Frequentie (F):
f =(1,88 x 10^6 m / s) / (3,46 x 10^-10 m) ≈ 5,43 x 10^15 Hz
Daarom is de frequentie van de materiegolf geassocieerd met een 10 eV-vrij elektron ongeveer 5,43 x 10^15 Hz en de golflengte is ongeveer 3,46 x 10^-10 m.
 Bacteriën kapen latente faag van concurrent
Bacteriën kapen latente faag van concurrent Wat is de kleur van het gas dat wordt gevormd door koper en salpeterzuur te combineren?
Wat is de kleur van het gas dat wordt gevormd door koper en salpeterzuur te combineren?  Reactie voegt chirale groepen toe aan stikstofringen zonder eerst reactieve groepen te installeren
Reactie voegt chirale groepen toe aan stikstofringen zonder eerst reactieve groepen te installeren Zijn zoutzuur en Muriatic hetzelfde?
Zijn zoutzuur en Muriatic hetzelfde?  Science Fair-projecten voor longcapaciteit
Science Fair-projecten voor longcapaciteit
Hoofdlijnen
- Geluidsoverlast schaadt dieren, en we weten niet eens hoeveel
- Wat produceert de voorafheid van eiwitten vooraf?
- Alternatieve evolutie:waarom je eigen genen veranderen als je die van iemand anders kunt lenen?
- Welke orgaansystemen vervullen onderling samenhangende functies in het menselijk lichaam?
- Wat is het aantal chromosomen in een edelsteen?
- Wat de sense organen die het bericht ontvangen en handelen?
- Onderzoek naar de trends waarmee de Europese landbouw te maken zal krijgen
- De enige factor die een wetenschapper verandert tijdens een experiment, ook wel onafhankelijke variabele genoemd?
- Hoe het genoom zijn functionele microarchitectuur bepaalt
- Deep learning en metamaterialen maken het onzichtbare zichtbaar

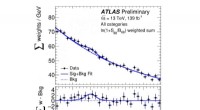
- ATLAS-experiment zoekt naar zeldzaam Higgs-boson vervalt in een foton en een Z-boson
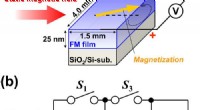
- Technologie voor het oogsten van energie op basis van ferromagnetische resonantie
- Bio-circuit bootst synapsen en neuronen na in een stap in de richting van sensorisch computergebruik
- Quantuminformatie overdragen met geluid
 Op zoek naar de beste 3D-printmaterialen
Op zoek naar de beste 3D-printmaterialen Atmosferische wetenschappers ronden het winterwolkenzaaiproject af in het zuidwesten van Idaho
Atmosferische wetenschappers ronden het winterwolkenzaaiproject af in het zuidwesten van Idaho Wat is een gasachtige toestand van materie die bestaat uit vrije elektronen en atoomkernen?
Wat is een gasachtige toestand van materie die bestaat uit vrije elektronen en atoomkernen?  Zoals huishoudfolie, nieuw biomateriaal kan lastige brandwonden bedekken en infecties blokkeren
Zoals huishoudfolie, nieuw biomateriaal kan lastige brandwonden bedekken en infecties blokkeren Wat zijn de verschillen tussen nuttige en verspilde energie?
Wat zijn de verschillen tussen nuttige en verspilde energie?  Kan een tropische watervlo Europese meren binnendringen?
Kan een tropische watervlo Europese meren binnendringen?  Verrassingsbevinding suggereert dat waterwerelden vaker voorkomen dan we dachten
Verrassingsbevinding suggereert dat waterwerelden vaker voorkomen dan we dachten Heeft een gloeilamp mechanische energie?
Heeft een gloeilamp mechanische energie?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

