
Wetenschap
Hoe bepaal je de grootte en richting van resulterende niet -contracterende krachten?
1. Kies een handig coördinatensysteem:
* Selecteer een X-Y-coördinatensysteem dat aansluit bij de krachten voor gemakkelijkere berekeningen.
* Als de krachten in 3D-ruimte zijn, heb je een X-Y-Z-coördinatensysteem nodig.
2. Los elke kracht op in zijn componenten:
* Breek elke kracht af in zijn horizontale (x) en verticale (y) componenten.
* Gebruik trigonometrie (sinus en cosinus) om de componenten te vinden:
* Horizontale component (x) =kracht * cos (hoek)
* Verticale component (y) =kracht * sin (hoek)
* Voor 3D-krachten moet je ook de z-component vinden.
3. Sum de componenten:
* Voeg alle horizontale componenten (x) samen toe. Dit geeft u de resulterende horizontale component (RX).
* Voeg alle verticale componenten (y) samen toe. Dit geeft u de resulterende verticale component (RY).
* Voeg voor 3D-krachten alle z-componenten toe om de resulterende Z-component (RZ) te vinden.
4. Bereken de grootte van de resulterende kracht:
* Gebruik de stelling van Pythagoras om de grootte van de resulterende kracht (R) te vinden:
* R =√ (rx² + ry²) (voor 2D -krachten)
* R =√ (rx² + ry² + rz²) (voor 3D -krachten)
5. Bepaal de richting van de resulterende kracht:
* Gebruik trigonometrie om de hoek (θ) van de resulterende kracht te vinden ten opzichte van de x-as:
* θ =tan⁻¹ (ry/rx) (voor 2D -krachten)
* Voor 3D -krachten moet je de hoeken vinden ten opzichte van elke as (x, y en z).
Voorbeeld:
Laten we zeggen dat je twee krachten hebt:
* Kracht 1:10 n bij 30 ° boven de horizontale.
* Kracht 2:5 n bij 60 ° onder de horizontale.
1. Componenten:
* Force 1:
* X-component =10 n * cos (30 °) =8,66 n
* y-component =10 n * sin (30 °) =5 n
* Force 2:
* X-component =5 n * cos (60 °) =2,5 n
* y -component =5 n * sin (60 °) =-4.33 n (negatief omdat het onder de horizontale is)
2. Componenten samenvatten:
* Rx =8,66 n + 2,5 n =11,16 n
* Ry =5 n - 4,33 n =0,67 n
3. Magnitude van resultant:
* R =√ (11.16² + 0.67²) =11,19 n
4. Richting van resulterende:
* θ =tan⁻¹ (0,67/11.16) =3,4 ° boven de horizontale.
Daarom heeft de resulterende kracht een grootte van 11,19 N en werkt hij onder een hoek van 3,4 ° boven de horizontale.
Belangrijke opmerking:
* De richting van de resulterende kracht wordt meestal uitgedrukt als een hoek ten opzichte van een gekozen referentieas (vaak de horizontale as).
* Wanneer u met 3D -krachten werkt, moet u de hoeken vinden ten opzichte van elke as (x, y en z). Dit kan worden gedaan met behulp van het puntproduct tussen de resulterende krachtvector en de eenheidsvectoren langs elke as.
* Het is belangrijk om aandacht te schenken aan de tekenen van de componenten, omdat ze het kwadrant van de resulterende kracht bepalen.
 Hoe planten hun groenheid afstemmen op de lichtkwaliteit
Hoe planten hun groenheid afstemmen op de lichtkwaliteit  Ocean Health Index publiceert zevende jaarlijkse beoordeling van wereldwijde oceaangezondheid
Ocean Health Index publiceert zevende jaarlijkse beoordeling van wereldwijde oceaangezondheid Waar wordt het water gedistribueerd tijdens een droogte?
Waar wordt het water gedistribueerd tijdens een droogte?  Onaanvaardbare kosten:savanneverbranding onder het Australische koolstofkredietschema schaadt de menselijke gezondheid
Onaanvaardbare kosten:savanneverbranding onder het Australische koolstofkredietschema schaadt de menselijke gezondheid Welke risico's kunnen huisdierenhamsters en gerbils in Australië met zich meebrengen?
Welke risico's kunnen huisdierenhamsters en gerbils in Australië met zich meebrengen?
Hoofdlijnen
- Hoe de pest werkt
- Evolutie in je achtertuin - koolmezen passen hun snavel misschien aan aan vogelvoeders
- Apple-CEO Tim Cook legt uit waarom hij zich uitsprak over immigratie
- Kunnen de vocalisaties van chimpansees de oorsprong van de menselijke taal onthullen?
- Hoe reproduceren protisten?
- De kracht van natuurlijke landschappen benutten om ongedierte uit te roeien
- Het is moeilijk om fossiele huid te vinden, maar een zeldzame ontdekking onthult aanwijzingen over de evolutie van water naar land
- De wetenschap bevestigt wat we allemaal weten:gentrificatie treft minderheden onevenredig zwaar
- Zijn de vadergenen altijd dominante genen?
- Nieuw pad voorgesteld voor kernfusie
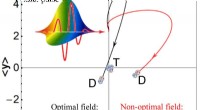
- Het mysterie van verstrengelde lichtdeeltjes opsporen

- Radioactieve moleculen kunnen het mysterie van ontbrekende antimaterie helpen oplossen
- Concept van nul is eeuwen ouder dan aangenomen,

- Nieuwe optische methode maakt de weg vrij voor ademtest voor biomarker voor kanker

 Neutronen helpen de viscositeit van celmembranen te meten en onthullen de basis ervan
Neutronen helpen de viscositeit van celmembranen te meten en onthullen de basis ervan In een nabijgelegen melkwegstelsel, een snelle radio-uitbarsting ontrafelt meer vragen dan antwoorden
In een nabijgelegen melkwegstelsel, een snelle radio-uitbarsting ontrafelt meer vragen dan antwoorden Wat loopt de Melkweg Galaxy door het centrum van welk sterrenbeeld?
Wat loopt de Melkweg Galaxy door het centrum van welk sterrenbeeld?  Een nieuwe nanobio-katalysator voor biobrandstoffen
Een nieuwe nanobio-katalysator voor biobrandstoffen Wordt er een product gevormd wanneer Bao en H2O samen reageren?
Wordt er een product gevormd wanneer Bao en H2O samen reageren?  Deepfakes:vijf manieren waarop ze briljante zakelijke kansen zijn
Deepfakes:vijf manieren waarop ze briljante zakelijke kansen zijn Waarom raken meer meteoren de maan dan de aarde?
Waarom raken meer meteoren de maan dan de aarde?  Spinnen besproeid met koolstofnanobuisjes spinnen supersterke webben
Spinnen besproeid met koolstofnanobuisjes spinnen supersterke webben
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

