
Wetenschap
Welke twee beginnen beide uit rust en hebben dezelfde constante versnelling wanneer radar wordt gebruikt om de snelheid van elke auto te meten en wordt op onmiddellijk twee keer zo snel B beweeg?
Inzicht in de situatie
* Twee auto's (A en B) Start vanaf rust: Dit betekent dat hun beginsnelheden nul zijn (v₀ =0).
* Constante versnelling: Beide auto's ervaren dezelfde snelheid van verandering in snelheid.
* Radar meet snelheid: Dit geeft ons op een specifiek moment de momentane snelheid van elke auto.
* Auto A is twee keer zo snel als auto B: Dit betekent dat de snelheid van auto A het dubbele is van de snelheid van auto B op het moment dat de radarmeting wordt genomen.
Het probleem instellen
Laten we de volgende variabelen gebruiken:
* VA: Snelheid van auto a
* vb: Snelheid van auto B
* a: Constante versnelling (hetzelfde voor beide auto's)
* t: Tijd verstreken
De bewegingsvergelijkingen gebruiken
We kunnen de volgende bewegingsvergelijking gebruiken, die snelheid, initiële snelheid, versnelling en tijd relateert:
* v =v₀ + bij
Omdat beide auto's beginnen bij rust (v₀ =0), vereenvoudigt de vergelijking tot:
* v =AT
De informatie toepassen op het probleem
1. Auto A is twee keer zo snel als auto B:
* VA =2VB
2. Gebruik van de bewegingsvergelijking voor beide auto's:
* va =at
* vb =op
Oplossen voor tijd
Nu hebben we twee vergelijkingen en twee onbekenden (VA en VB). We kunnen voor de tijd (t) oplossen wanneer de radarmeting is genomen:
1. Vervang va =2VB in de vergelijking va =op:
* 2VB =AT
2. Aangezien VB =AT, kunnen we dit vervangen door de bovenstaande vergelijking:
* 2 (AT) =AT
3. Vereenvoudig en los op voor t:
* 2at =op
* 2at - op =0
* op =0
* Aangezien versnelling (a) constant is en niet nul is, is de enige manier waarop deze vergelijking waar kan zijn, als t =0 .
Conclusie
Dit betekent dat de radarmeting op het moment dat de auto's begonnen te bewegen (t =0) is genomen. Op dat moment zouden beide auto's een snelheid van nul hebben, hoewel auto A twee keer zo snel zou bewegen als auto B. Dit komt omdat de radarmeting een onmiddellijke lezing is, en aan het begin van hun beweging zijn beide auto's nog steeds in rust.
 Op fosfor gebaseerde composieten als anodematerialen voor kalium-ionbatterijen
Op fosfor gebaseerde composieten als anodematerialen voor kalium-ionbatterijen Hoeveel meer valance -elektronen heeft zuurstof nodig om een volledige buitenste valentieschaal te hebben?
Hoeveel meer valance -elektronen heeft zuurstof nodig om een volledige buitenste valentieschaal te hebben?  Zouden zwavel en zuurstof een ionische moleculaire of zure chemische binding vormen?
Zouden zwavel en zuurstof een ionische moleculaire of zure chemische binding vormen?  Team ontwikkelt innovatieve, ideale vloeistofafstotende oppervlakken
Team ontwikkelt innovatieve, ideale vloeistofafstotende oppervlakken Wat is de chemische reactie tussen calciumhydroxide en koolstofdioxide?
Wat is de chemische reactie tussen calciumhydroxide en koolstofdioxide?
 Nieuwe studiemodellen impact stijgende fossiele brandstofprijzen op werkgelegenheid
Nieuwe studiemodellen impact stijgende fossiele brandstofprijzen op werkgelegenheid Kameleon-oceaanbacteriën kunnen van kleur veranderen
Kameleon-oceaanbacteriën kunnen van kleur veranderen Menselijke activiteiten drogen de Amazone uit:NASA-studie
Menselijke activiteiten drogen de Amazone uit:NASA-studie Ons vermogen om zich bewust te zijn van sommige delen die onze omgeving terwijl het negeren andere wordt genegeerd, wordt gebeld?
Ons vermogen om zich bewust te zijn van sommige delen die onze omgeving terwijl het negeren andere wordt genegeerd, wordt gebeld?  NASA ziet tropische cycloon Debbie Queensland naderen voor aanlanding
NASA ziet tropische cycloon Debbie Queensland naderen voor aanlanding
Hoofdlijnen
- Nu weten we waarom wortels oranje zijn
- Welk model beschrijft het kenmerk van celmembraan?
- Waarom zijn pygmeeën klein?
- Onderzoek met bacteriën brengt wetenschappers een stap dichter bij het maken van kunstmatige cellen met levensechte functionaliteit
- Waar wordt ATP het meest efficiënt geproduceerd?
- Onbeleefdheid op het werk:wordt het 'koninginbijensyndroom' erger?
- Wat is de functie van restrictie -enzymen in proces -DNA -recombinatie?
- Waarom kunnen de onderzoeken van Robert Hooke en Anton van Leeuwenhoek worden beschouwd als een begin van microscopiemicrobiologie?
- Waarom is het belangrijk dat een hypothese wordt gestart, dus kan worden gewijzigd?
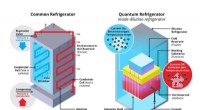
- Onderzoekers ontwikkelen supergeleidende kwantumkoelkast
- Ingenieurs produceren baanbrekende sensor voor fotografie, levenswetenschappen, veiligheid

- Buigzame laserstralen kunnen menselijk weefsel onderzoeken als nooit tevoren

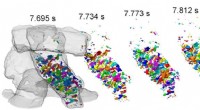
- 'S Werelds snelste 3D-tomografische beelden gerapporteerd op BESSY II
- Lichtgewicht hyperspectrale imagers brengen geavanceerde beeldvormingscapaciteit naar drones

 Hoe te omzetten Radian naar Minuten
Hoe te omzetten Radian naar Minuten  Wat is het ware bacteriënrijk?
Wat is het ware bacteriënrijk?  Wat vergelijkt de hoeveelheid energie voor en na een conversie is het aerodynamische vorm B -efficiëntie of wrijving?
Wat vergelijkt de hoeveelheid energie voor en na een conversie is het aerodynamische vorm B -efficiëntie of wrijving?  Het transformeren van genderverhoudingen de sleutel tot bloei op oudere leeftijd, onderzoekers zeggen:
Het transformeren van genderverhoudingen de sleutel tot bloei op oudere leeftijd, onderzoekers zeggen: Hoe gebruikt plaque suiker?
Hoe gebruikt plaque suiker?  Nieuw lab-on-a-chip-platform wil de detectie van pathogenen verbeteren
Nieuw lab-on-a-chip-platform wil de detectie van pathogenen verbeteren Milieuvriendelijk gedrag is gemakkelijk - toeristen hebben alleen een duwtje nodig
Milieuvriendelijk gedrag is gemakkelijk - toeristen hebben alleen een duwtje nodig De fouten in klimaatmodellen uitroeien om orkanen beter te voorspellen
De fouten in klimaatmodellen uitroeien om orkanen beter te voorspellen
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

