
Wetenschap
Berekenen hoe kwantumtoestanden elkaar overlappen
Hier ziet u hoe de overlap van kwantumtoestanden wordt berekend:
Beschouw twee kwantumtoestanden die worden weergegeven door hun golffuncties, \(\psi_1(x)\) en \(\psi_2(x)\). De overlap tussen deze toestanden wordt gegeven door de overlapintegraal:
$$ \taal \psi_1 | \psi_2 \rangle =\int_{-\infty}^\infty \psi_1^*(x) \psi_2(x) \ dx $$
waarbij \(\psi_1^*(x)\) de complexe conjugaat is van \(\psi_1(x)\).
De overlapintegraal berekent de gewogen integraal van het product van de twee golffuncties over het gehele domein. Het resultaat is een complex getal, en de absolute waarde ervan in het kwadraat geeft de waarschijnlijkheid aan dat een deeltje in de toestand \(\psi_1\) zal worden aangetroffen in de toestand \(\psi_2\), indien gemeten.
Belangrijke punten om op te merken:
- De overlapintegraal is een maatstaf voor de gelijkenis tussen twee kwantumtoestanden. Het varieert van 0 tot 1, waarbij 0 orthogonale toestanden (totaal verschillend) aangeeft en 1 identieke toestanden aangeeft.
- Voor genormaliseerde golffuncties vertegenwoordigt de overlapintegraal de waarschijnlijkheidsamplitude voor het vinden van een deeltje in toestand \(\psi_1\) terwijl het zich in toestand \(\psi_2\) bevindt.
- Overlappende kwantumtoestanden spelen een cruciale rol bij kwantuminterferentie, verstrengeling en andere fundamentele kwantumverschijnselen.
- Bij kwantumcomputing worden overlappende toestanden gebruikt bij operaties zoals kwantumtoestandstomografie, kwantumteleportatie en kwantumfoutcorrectie.
- Bij het berekenen van de overlapintegraal zijn vaak numerieke integratiemethoden voor ingewikkelde golffuncties nodig.
Voorbeelden:
- Voor twee identieke golffuncties is de overlap 1:
$$ \taal \psi | \psi \rangle =\int_{-\infty}^\infty |\psi(x)|^2 \ dx =1$$
- Voor orthogonale toestanden is de overlap 0:
$$ \taal \psi_1 | \psi_2 \rangle =\int_{-\infty}^\infty \psi_1^*(x) \psi_2(x) \ dx =0 $$
Deze voorbeelden illustreren de basisprincipes van het berekenen van de overlap tussen kwantumtoestanden. Toepassingen in de echte wereld vereisen mogelijk complexere golffuncties en integratiemethoden, maar het fundamentele concept blijft hetzelfde.
 Nieuwe ontwikkelingen in het zoeken naar moleculaire magneten
Nieuwe ontwikkelingen in het zoeken naar moleculaire magneten Plantafweerlaag heeft onverwacht effect op vluchtige stoffen, studie vondsten
Plantafweerlaag heeft onverwacht effect op vluchtige stoffen, studie vondsten Nieuwe klasse zonnecellen, gebruik van loodvrije perovskietmaterialen
Nieuwe klasse zonnecellen, gebruik van loodvrije perovskietmaterialen Onderzoek toont aan dat afzonderlijke atomen efficiëntere katalysatoren kunnen maken
Onderzoek toont aan dat afzonderlijke atomen efficiëntere katalysatoren kunnen maken Het nieuwe peptide van biologen kan veel kankers bestrijden
Het nieuwe peptide van biologen kan veel kankers bestrijden
 NASA-satelliettemperaturen onthullen een sterkere orkaan Lee
NASA-satelliettemperaturen onthullen een sterkere orkaan Lee Uit onderzoek blijkt dat aardbevingen nog jaren doorgaan nadat de injectie van afvalwater in het gasveld is gestopt
Uit onderzoek blijkt dat aardbevingen nog jaren doorgaan nadat de injectie van afvalwater in het gasveld is gestopt Europese steden hebben te maken met extremer weer dan eerder werd gedacht
Europese steden hebben te maken met extremer weer dan eerder werd gedacht Monitoring lavameerniveaus in Congo-vulkaan
Monitoring lavameerniveaus in Congo-vulkaan Bossen en mensen beschermen tegen tropische stormen
Bossen en mensen beschermen tegen tropische stormen
Hoofdlijnen
- Definitie van biologische opvolging
- Hoe stamcellen werken
- Rangschikken met behulp van een vierkantswortelcurve
- Nieuwe inzichten helpen verklaren waarom seksuele interacties tussen mensen van hetzelfde geslacht zo belangrijk zijn voor vrouwelijke bonobo's
- Een kungfu-kick leidde onderzoekers naar 's werelds oudste complete visfossielen. Dit is wat ze hebben gevonden
- Twee fasen van fotosynthese
- Oude haai uit China is misschien wel de oudste voorouder met kaken van de mens
- Vijf soorten isolatie in de biologie
- Hoe het leven op het land leerde ademen
- ALPHA observeert voor het eerst het lichtspectrum van antimaterie

- Willekeurig dicht verpakken of vastlopen van bollen in een container
- Apparaatontwerp maakt een tienvoudige toename van spinstromen mogelijk
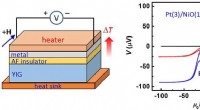
- Molecuul-gemedieerde oppervlaktereconstructie maakt gigantische opconversie luminescentieverbetering mogelijk
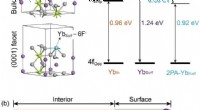
- Onconventionele supergeleider speelt de rol van een veelbelovend kwantumcomputerplatform
 Astronomen ontdekken klasse van vreemde objecten in de buurt van het enorme zwarte gat van ons melkwegstelsel
Astronomen ontdekken klasse van vreemde objecten in de buurt van het enorme zwarte gat van ons melkwegstelsel Uit waarnemingen blijkt dat J0526+5934 een dubbele witte dwerg met een ultrakorte periode is
Uit waarnemingen blijkt dat J0526+5934 een dubbele witte dwerg met een ultrakorte periode is  Metingen van botsingen met hoge energie leiden tot een beter begrip van waarom mesondeeltjes verdwijnen
Metingen van botsingen met hoge energie leiden tot een beter begrip van waarom mesondeeltjes verdwijnen  Voorbeelden van archaebacteriën met hun wetenschappelijke naam en classificatie
Voorbeelden van archaebacteriën met hun wetenschappelijke naam en classificatie leraren, pedagogische vaardigheden, en het obstakel van intuïtie
leraren, pedagogische vaardigheden, en het obstakel van intuïtie Nieuwe inzichten in waarom verbeteringen aan Chesapeake Bay een uitdaging blijven
Nieuwe inzichten in waarom verbeteringen aan Chesapeake Bay een uitdaging blijven  Hoe hebben leeuwen zich aan hun omgeving aangepast?
Hoe hebben leeuwen zich aan hun omgeving aangepast?  Ultradunne kwantumlichtbronnen:wetenschappers tonen aan dat excitonische interacties de efficiëntie van de generatie van verstrengelde fotonen verhogen
Ultradunne kwantumlichtbronnen:wetenschappers tonen aan dat excitonische interacties de efficiëntie van de generatie van verstrengelde fotonen verhogen
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

