
Wetenschap
Een horizontale kracht van grootte F 120 N wordt gebruikt om een doosmassa m 7 kg van rustafstand D 15 omhoog wrijvingsloze helling met helling Q 34 te duwen?
1. Definieer het systeem en krachten
* Systeem: De doos
* krachten:
* toegepaste kracht (f): 120 n, horizontaal
* zwaartekracht (mg): Handelt verticaal naar beneden
* Normale kracht (N): Wandelt loodrecht op de helling en balanceert de component van de zwaartekracht loodrecht op de helling.
* Component van zwaartekracht parallel aan de helling (Mg sin θ): Deze component werkt om zich te verzetten tegen de toegepaste kracht.
2. Gratis lichaamsdiagram
Teken een vrij lichaamsdiagram om de krachten op de doos te visualiseren.
3. Krachten oplossen
* Los de zwaartekracht op:
* De component van de zwaartekracht parallel aan de helling is mg sin θ.
* Het onderdeel van de zwaartekracht loodrecht op de helling is mg cos θ.
* Los de toegepaste kracht op:
* De component van de uitgeoefende kracht parallel aan de helling is f cos θ.
* De component van de uitgeoefende kracht loodrecht op de helling is f sin θ.
4. Pas de tweede wet van Newton toe
* de tweede wet van Newton (langs de helling): Σf =ma
* Netto kracht langs de helling: F cos θ - mg sin θ =ma
5. Oplossen voor versnelling
* Vervang de gegeven waarden:120 n * cos (34 °) - (7 kg * 9,8 m/s² * sin (34 °)) =(7 kg) * a
* Bereken de versnelling (a).
6. Gebruik kinematica om definitieve snelheid te vinden
* Kinematics -vergelijking: v² =u² + 2As
* Initiële snelheid (u): 0 m/s (begint vanaf rust)
* Afstand (s): 15 m
* versnelling (a): U berekende dit in stap 5.
* Oplossen voor de uiteindelijke snelheid (V).
Laten we de antwoorden berekenen:
* versnelling:
* 120 n * cos (34 °) - (7 kg * 9,8 m/s² * sin (34 °)) =(7 kg) * a
* A ≈ 2,95 m/s²
* Eindsnelheid:
* v² =0² + 2 * 2,95 m/s² * 15 m
* V ≈ 9.49 m/s
Daarom is de uiteindelijke snelheid van de doos nadat hij 15 meter omhoog is geduwd, de helling is ongeveer 9,49 m/s.
 Theoretisch perspectief op C-H/O-H activering door Cu-O in biologische en synthetische systemen
Theoretisch perspectief op C-H/O-H activering door Cu-O in biologische en synthetische systemen Groen cement een stap dichter bij een game-changer voor bouwemissies
Groen cement een stap dichter bij een game-changer voor bouwemissies Hoe illustreert u chemische verandering versus fysiek in een Venn -diagram?
Hoe illustreert u chemische verandering versus fysiek in een Venn -diagram?  Hoe men één deeloplossing mengt met vier delen water
Hoe men één deeloplossing mengt met vier delen water  Een zure oplossing reageert met magnesiumcarbonaat om een gas te produceren Wat is de formule voor gas?
Een zure oplossing reageert met magnesiumcarbonaat om een gas te produceren Wat is de formule voor gas?
 Onderzoek eerst om de impact van de evolutie op ecosystemen aan te tonen
Onderzoek eerst om de impact van de evolutie op ecosystemen aan te tonen  Nauwkeurige gegevens voor verbeterde kustbescherming
Nauwkeurige gegevens voor verbeterde kustbescherming Vulkaan Bali spuwt as bij nieuwe uitbarsting
Vulkaan Bali spuwt as bij nieuwe uitbarsting Nieuwe kijk op de wereld kan onbeperkte duurzame hulpbronnen creëren
Nieuwe kijk op de wereld kan onbeperkte duurzame hulpbronnen creëren Er worden hulpmiddelen aangeboden om te bepalen hoeveel voldoende is bij het besproeien van het gras
Er worden hulpmiddelen aangeboden om te bepalen hoeveel voldoende is bij het besproeien van het gras
Hoofdlijnen
- Wat is het gebruik van beker?
- Wiskunde laat zien hoe menselijk gedrag infectieziekten verspreidt
- Hoe werken abiotische en biotische factoren samen in het ecosysteem?
- Wat zijn drie redenen om DNA uit een menselijk onderwerp te extraheren?
- Welke organische verbinding bevat informatie van de ene generatie op de volgende tijdens de reproductie?
- Zullen planten zich alleen reproduceren met leden van dezelfde soort?
- Hoe interageren producentenconsumentencomposers met de abiotische factoren in het ecosysteem?
- Wat zijn de structuren en functies van het perifere systeem van het centrale zenuwstelsel?
- Nieuwe richtlijnen voor bestuivers zijn bedoeld om Ierlands landbouwgrond weer levendig te maken
- Verbeterde frequentieverdubbeling draagt bij aan de fotonica-toolkit
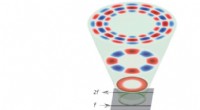
- Onderzoekers creëren een praktisch en veelzijdig microscopisch optomechanisch apparaat

- Gebruik van een antineutrino-reactor-off-methode tussen onderzeese patrouilles om de behoefte aan toegangsinspecties aan boord te omzeilen

- Fotonische stralingssensoren overleven enorme doses onbeschadigd

- Onderzoekers suggereren een nieuwe manier om een lichtbron te genereren die is gemaakt van verstrengelde fotonen

 Nieuwe metingen werpen licht op de impact van watertemperaturen op het afkalven van gletsjers
Nieuwe metingen werpen licht op de impact van watertemperaturen op het afkalven van gletsjers Eerste directe bandafstandmetingen van waterstof met brede kloof met behulp van inelastische röntgenverstrooiing
Eerste directe bandafstandmetingen van waterstof met brede kloof met behulp van inelastische röntgenverstrooiing Was koolstoftetrachloride in de jaren 60 door de Amerikaanse marine gebruikt?
Was koolstoftetrachloride in de jaren 60 door de Amerikaanse marine gebruikt?  Hoe de onderlinge afhankelijkheid van levende organismen te beschrijven
Hoe de onderlinge afhankelijkheid van levende organismen te beschrijven Hoe kunnen we afstanden met sterren en sterrenstelsels in ons universum meten?
Hoe kunnen we afstanden met sterren en sterrenstelsels in ons universum meten?  Natuurkundigen leggen uit waarom supergeleiders er niet in slagen superstromen te produceren
Natuurkundigen leggen uit waarom supergeleiders er niet in slagen superstromen te produceren  Voedingsgedrag kan een indicator zijn van voerefficiëntie bij Holstein-koeien
Voedingsgedrag kan een indicator zijn van voerefficiëntie bij Holstein-koeien Orgelsystemen die betrokken zijn bij homeostase
Orgelsystemen die betrokken zijn bij homeostase
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap & Ontdekkingen © https://nl.scienceaq.com

