
Wetenschap
Wat is de straal van halve cirkel in een cyclotron als Deutron waar M gelijk is aan 3.3410-27 kg verwerft 15 MeV-energie gegeven B 1,5 t?
1. Begrijp de concepten:
* cyclotron: Een cyclotron is een apparaat dat geladen deeltjes versnelt met behulp van een magnetisch veld. De deeltjes bewegen in een spiraalvormig pad als gevolg van de magnetische kracht.
* Deuteron: Een deuteron is de kern van een deuteriumatoom, bestaande uit één proton en één neutron.
* Kinetische energie: De energie die door de Deuteron is opgedaan, is de kinetische energie (KE).
2. Relevante vergelijkingen:
* Kinetische energie: Ke =(1/2) mv²
* magnetische kracht op een geladen deeltje: F =QVB
* Centripetal Force: F =mv²/r
3. Stappen om de straal te berekenen:
* Energie converteren naar joules: 15 MeV =15 × 10⁻³ EV =15 × 10⁻³ × 1.602 × 10⁻¹⁹ J
* Vind de snelheid van de Deuteron:
* Ke =(1/2) mv²
* v =√ (2Ke / m) =√ (2 × 15 × 10⁻³ × 1.602 × 10⁻¹⁹ J / 3.34 × 10⁻²⁷ kg)
* Eigen magnetische kracht met centripetale kracht: De magnetische kracht op de Deuteron houdt het in een cirkelvormig pad, wat de centripetale kracht is.
* qvb =mv²/r
* Los op voor de straal:
* r =mv / (qb) =(3,34 × 10⁻²⁷ kg × √ (2 × 15 × 10⁻³ × 1.602 × 10⁻¹⁹ j / 3.34 × 10⁻²⁷ kg)) / (1.602 × 10⁻¹⁹ C × 1.5 t)
4. Berekening:
Nadat u de waarden hebt aangesloten en de berekening heeft uitgevoerd, zult u merken dat de straal (R) van de halve cirkel ongeveer is:
r ≈ 0,012 meter of 1,2 centimeter
belangrijke opmerkingen:
* De lading van een deuteron (q) is hetzelfde als de lading van een proton:1.602 × 10⁻¹⁹ Coulombs.
* Zorg ervoor dat u tijdens de berekening consistente eenheden gebruikt.
* Deze berekening veronderstelt dat de Deuteron met een constante snelheid in een cirkelvormig pad beweegt.
Laat het me weten als je nog andere vragen hebt!
 Wat is een subtropische storm en hoe verschilt deze van een tropisch of extratropisch systeem?
Wat is een subtropische storm en hoe verschilt deze van een tropisch of extratropisch systeem?  Verouderde dammen zijn de sleutel tot de waterkwaliteit
Verouderde dammen zijn de sleutel tot de waterkwaliteit Menselijk gedrag moet worden meegenomen in analyses van klimaatverandering
Menselijk gedrag moet worden meegenomen in analyses van klimaatverandering Vredesakkoord Colombia vormt een nieuwe bedreiging voor het regenwoud van het land
Vredesakkoord Colombia vormt een nieuwe bedreiging voor het regenwoud van het land Klimaattechniek brengt ernstige nationale veiligheidsrisico's met zich mee; landen die met extreme hitte te maken hebben, kunnen het hoe dan ook proberen
Klimaattechniek brengt ernstige nationale veiligheidsrisico's met zich mee; landen die met extreme hitte te maken hebben, kunnen het hoe dan ook proberen
Hoofdlijnen
- Wat is het fenomeen dat bekend staat wanneer cell water verliest door osmose?
- Wat is de koloniemorfologie van Bacillus Cereus?
- Waarom wordt DNA gekopieerd vóór mitose?
- Wetenschappers verbeteren voorspellingen over hoe de temperatuur de overlevingsvisembryo's beïnvloedt
- Waar zijn cel -enzymen van gemaakt?
- Kunnen eiwitten afzonderlijke domeinen hebben met verschillende structuren en functies?
- Hoe wordt de studie van wormen genoemd?
- De genetische code stuurt de synthese van honderden verschillende soorten?
- Waarom studeer je evolutie?
- Deze technologie voor het maken van regenboog kan autonome voertuigen helpen borden te lezen

- Wetenschappers vinden oppervlakte-emitterende laser met topologische holte uit

- Chiraliteit-ondersteunde laterale impulsoverdracht voor bidirectionele enantioselectieve scheiding

- 's Werelds eerste zelfgekalibreerde fotonische chip:een uitwisseling voor optische datasnelwegen
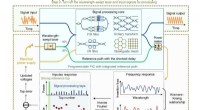
- De grenzen van meetnauwkeurigheid opnieuw definiëren

 Inprenten van nanopatronen in metalen
Inprenten van nanopatronen in metalen Dunne waterlagen zijn veelbelovend voor de energieopslag van de toekomst
Dunne waterlagen zijn veelbelovend voor de energieopslag van de toekomst Statistici zeggen dat Brazilië tegen Duitsland zal spelen in de FIFA Wereldbekerfinale
Statistici zeggen dat Brazilië tegen Duitsland zal spelen in de FIFA Wereldbekerfinale Leven buiten de aarde? Onderwatergrotten op de Bahama's kunnen aanwijzingen geven
Leven buiten de aarde? Onderwatergrotten op de Bahama's kunnen aanwijzingen geven  Brexit heeft de gemiddelde werknemer al meer dan een week loon gekost, academische studie toont
Brexit heeft de gemiddelde werknemer al meer dan een week loon gekost, academische studie toont Op welke manieren verschillen meteoren van asteroïden?
Op welke manieren verschillen meteoren van asteroïden?  Wat maakt Titan uniek onder de manen van het zonnestelsel?
Wat maakt Titan uniek onder de manen van het zonnestelsel?  De zware vrachtwagens in Californië hoeven niet door smog te worden gecontroleerd. Waarom dat over verandering gaat
De zware vrachtwagens in Californië hoeven niet door smog te worden gecontroleerd. Waarom dat over verandering gaat
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap & Ontdekkingen © https://nl.scienceaq.com

