
Wetenschap
Vectormethode om erachter te komen de versnelling van een deeltje is -wwhe Angular Snelheid W?
Inzicht in de concepten
* Circulaire beweging: Wanneer een deeltje in een cirkelvormig pad beweegt, verandert de richting ervan constant, zelfs als de snelheid ervan constant is. Deze verandering in richting betekent dat er een versnelling is.
* hoeksnelheid (ω): Dit meet hoe snel het deeltje roteert. Het is de snelheid van verandering van de hoek (θ) ten opzichte van tijd (t):ω =dθ/dt.
* Centripetale versnelling (A c ): Deze versnelling is gericht op het midden van de cirkel en is verantwoordelijk voor het bewegen van het deeltje in een cirkelvormig pad.
het afleiden van de versnelling
1. Positievector: Laten we zeggen dat het deeltje zich op een positie bevindt r ten opzichte van het midden van de cirkel. Deze positie vector is een functie van de tijd: r (t) .
2. snelheidsvector: De snelheidsvector is de tijd afgeleide van de positievector: v (t) =dr (t)/dt . Omdat het deeltje in een cirkel beweegt, is de snelheid ervan altijd de cirkel.
3. versnellingsvector: De versnellingsvector is de tijd afgeleide van de snelheidsvector: a (t) =dv (t)/dt . Om de versnelling te vinden, moeten we de snelheidsvector onderscheiden.
4. Polaire coördinaten met behulp van: Het is handig om polaire coördinaten (r, θ) te gebruiken om de positie van het deeltje te beschrijven. In dit systeem:
* r is de radiale afstand vanaf het midden van de cirkel.
* θ is de hoek die de positievector maakt met een referentieas.
5. Snelheid tot uitdrukking brengen in polaire coördinaten:
* v =(dr/dt) * r̂ + (r * dθ/dt) * θ̂
* R̂ is de eenheidsvector in de radiale richting.
* θ̂ is de eenheidsvector in de tangentiële richting.
6. Versnelling tot uitdrukking brengen in polaire coördinaten:
* a =[(d²r/dt²) - (r * (dθ/dt) ²)] * r̂ + [(r * d²θ/dt²) + 2 * (dr/dt) * (dθ/dt)] * θ̂
7. Vereenvoudiging voor uniforme cirkelvormige beweging:
* Voor uniforme cirkelvormige beweging is de straal (R) constant, dus DR/dt =0 en d²r/dt² =0.
* Ook is hoeksnelheid (ω) constant, dus d²θ/dt² =0.
8. Eindresultaat:
* a =- (r * ω²) * r̂
Interpretatie:
* richting: De versnelling bevindt zich in de negatieve radiale richting (naar het midden van de cirkel).
* magnitude: De grootte van de versnelling is een c =r * ω². Dit is de centripetale versnelling.
Daarom wordt de versnelling van een deeltje die uniforme cirkelvormige beweging ondergaat, gegeven door - (r * ω²) * r̂, waarbij r de straal van de cirkel is en ω de hoeksnelheid is.
 Veelgebruikte chemische stof gekoppeld aan 100, 000 Amerikaanse sterfgevallen per jaar:studie
Veelgebruikte chemische stof gekoppeld aan 100, 000 Amerikaanse sterfgevallen per jaar:studie Circulaire wateroplossingen toepassen van India tot Zweden
Circulaire wateroplossingen toepassen van India tot Zweden Inwoners gewaarschuwd terwijl Louisiana zich schrap zet voor orkaan Ida
Inwoners gewaarschuwd terwijl Louisiana zich schrap zet voor orkaan Ida Oude mineralen recreëren
Oude mineralen recreëren Boreale bos- en toendragebieden zullen het zwaarst worden getroffen in de komende 500 jaar van klimaatverandering, zo blijkt uit het klimaatmodel
Boreale bos- en toendragebieden zullen het zwaarst worden getroffen in de komende 500 jaar van klimaatverandering, zo blijkt uit het klimaatmodel
Hoofdlijnen
- Stadsmuis of landmuis? Bioloog verzamelt muizen uit huizen om te onderzoeken hoe ze zo goed zijn geworden in het leven in de stad
- Onderzoek werpt nieuw licht op hoe ziekten over verschillende soorten heen springen
- Wat zijn de protozoa die niet in staat is tot onafhankelijke beweging?
- De volgorde die leidt naar de eerste eukaryotische cel?
- Onderzoek naar enzymatische chemische reacties kan erop wijzen hoe de eerste cellen kolonies vormden
- wat zijn de bestanddelen van voedsel?
- Wie was de botanicus die concludeerde dat alle planten uit cellen zijn samengesteld?
- Wat is het rootword van fotosynthese?
- Onderzoekers onthullen een nieuw mechanisme van hyaluronzuur met een specifiek molecuulgewicht om de ontsteking van de gastheer te verbeteren
- Onderzoekers ontwerpen compacte krachtige laser met behulp van plasma-optica

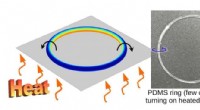
- Motoriserende vezels met geometrische nul-energiemodi
- Een snelle en gemakkelijke manier om instabiliteiten in fusie-apparaten te stoppen

- Wetenschappers voeren eerste ruimtegebaseerde meting uit van de levensduur van neutronen

- Natuurkundigen ontwikkelen aanpak om de prestaties van zonne-energie te verbeteren

 Groot, kristallijne lipide-scaffolds bieden nieuwe mogelijkheden voor eiwitten, drugsonderzoek
Groot, kristallijne lipide-scaffolds bieden nieuwe mogelijkheden voor eiwitten, drugsonderzoek Heeft de maan ooit een atmosfeer gehad?
Heeft de maan ooit een atmosfeer gehad?  Hoeveel punten moeten er in de Lewis-puntstructuur worden getekend voor een zuurstofatoom?
Hoeveel punten moeten er in de Lewis-puntstructuur worden getekend voor een zuurstofatoom?  Grafeen verhoogt de efficiëntie van zonnecellen van de volgende generatie
Grafeen verhoogt de efficiëntie van zonnecellen van de volgende generatie Hoe hedendaagse MBA-afgestudeerden kunnen helpen de wereld te redden
Hoe hedendaagse MBA-afgestudeerden kunnen helpen de wereld te redden Opnieuw een bovengemiddeld natuurbrandseizoen voor 2022. Hoe de klimaatverandering branden moeilijker te voorspellen en te bestrijden maakt.
Opnieuw een bovengemiddeld natuurbrandseizoen voor 2022. Hoe de klimaatverandering branden moeilijker te voorspellen en te bestrijden maakt.  In september gingen we voorbij de 1,5 graden. November, voor het eerst meer dan 2 graden. Wat is er aan de hand?
In september gingen we voorbij de 1,5 graden. November, voor het eerst meer dan 2 graden. Wat is er aan de hand?  Verborgen schoonheid van de nanokosmos
Verborgen schoonheid van de nanokosmos
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

