
Wetenschap
Hoe vind je de resulterende snelheid?
Inzicht in de resulterende snelheid
* snelheid: Snelheid beschrijft zowel de snelheid als de richting van de beweging van een object.
* resulterende snelheid: Dit is de algehele snelheid van een object wanneer het tegelijkertijd meerdere snelheden ervaart. Zie het als de "net" snelheid.
methoden om de resulterende snelheid te vinden
1. Vector -toevoeging (grafische methode):
* vertegenwoordigen snelheden als vectoren: Teken elke snelheid als een pijl. De lengte van de pijl vertegenwoordigt de grootte (snelheid) en zijn richting wijst in de bewegingsrichting.
* staart-to-head plaatsing: Plaats de staart van de tweede vector aan het hoofd van de eerste vector.
* Teken de resulterende: Teken een nieuwe vector uit de staart van de eerste vector naar de kop van de laatste vector. Dit vertegenwoordigt de resulterende snelheid.
* Meet de resulterende: Gebruik een liniaal en gradenboog om de grootte (lengte) en richting van de resulterende vector te bepalen.
2. Vector -toevoeging (wiskundige methode):
* Breek snelheden in componenten: Los elke snelheid op in horizontale (x) en verticale (y) componenten. U zult hiervoor trigonometrie (sinus, cosinus) gebruiken.
* Componenten toevoegen: Voeg de X-componenten samen en de Y-componenten samen toe.
* Vind magnitude: Gebruik de Pythagorische stelling om de grootte van de resulterende vector te berekenen:
* `Magnitude =√ ((σx) ² + (σy) ²)`
* Richting vinden: Gebruik de arctangent -functie om de hoek (richting) van de resulterende te vinden:
* `Angle =arctan (σy / σx)`
voorbeelden
Voorbeeld 1:Boat and Current
* Een boot reist om 10 km/u naar het oosten. Een stroom stroomt op 5 km/u naar het zuiden.
* grafisch: Teken de snelheid van de boot als een pijl van 10 km/u naar het oosten en de snelheid van de stroom als een pijl van 5 km/u naar het zuiden. Sluit de staart van de huidige vector aan op de kop van de bootvector. De resulterende vector wijst naar het zuidoosten.
* wiskundig:
* Boat Velocity (X, Y) =(10, 0)
* Stroomsnelheid (x, y) =(0, -5)
* Resulterende snelheid (x, y) =(10, -5)
* Magnitude =√ (10² + (-5) ²) ≈ 11,2 km/h
* Hoek =arctan (-5 / 10) ≈ -26,6 ° (ten zuiden van het oosten)
Voorbeeld 2:Projectielbeweging
* Een bal wordt gelanceerd bij 20 m/s in een hoek van 30 ° boven de horizontale.
* grafisch: Breek de beginsnelheid in horizontale (x) en verticale (y) componenten. De horizontale component blijft constant. De verticale component zal veranderen vanwege de zwaartekracht.
* wiskundig:
* Initiële snelheid (x, y) =(20 * cos (30 °), 20 * sin (30 °)) =(17.32, 10)
* U moet in de loop van de tijd rekening houden met veranderingen in de verticale snelheid als gevolg van de zwaartekracht.
Key Points
* richting is cruciaal: Snelheid is een vectorhoeveelheid, dus zowel snelheid als richting zijn belangrijk.
* Meerdere snelheden: De resulterende snelheid is van toepassing wanneer een object meer dan één snelheid tegelijkertijd ervaart.
* trigonometrie: Het gebruik van sinus, cosinus en raaklijn is vaak nodig om vectoren in componenten op te lossen.
Laat het me weten als je specifieke situaties hebt waar je door wilt werken!
 Wat zijn de actieve residuen in Dowex 2 en 50?
Wat zijn de actieve residuen in Dowex 2 en 50?  Onder welke omstandigheden zou waterstofbinding aanwezig zijn?
Onder welke omstandigheden zou waterstofbinding aanwezig zijn?  Wanneer de dichtheid het aantal moleculen in een volume toeneemt, varieert of blijft het hetzelfde?
Wanneer de dichtheid het aantal moleculen in een volume toeneemt, varieert of blijft het hetzelfde?  Is zilveren chloride polair of ionisch niet -polair?
Is zilveren chloride polair of ionisch niet -polair?  Welke twee producten worden gevormd als ijzersulfide in lucht wordt verwarmd?
Welke twee producten worden gevormd als ijzersulfide in lucht wordt verwarmd?
 Wat is een goede wetenschappelijke zin voor biosfeer?
Wat is een goede wetenschappelijke zin voor biosfeer?  Waarom leven apen in het regenwoud?
Waarom leven apen in het regenwoud?  De duikklok en de waterspin:hoe spinnen onder ademen
De duikklok en de waterspin:hoe spinnen onder ademen  Ontbrekende windvariabiliteit betekent dat toekomstige effecten van klimaatverandering in Europa en Noord-Amerika mogelijk worden onderschat
Ontbrekende windvariabiliteit betekent dat toekomstige effecten van klimaatverandering in Europa en Noord-Amerika mogelijk worden onderschat Hoe wolvenpersoonlijkheden wetlands kunnen veranderen
Hoe wolvenpersoonlijkheden wetlands kunnen veranderen
Hoofdlijnen
- Verbetering van de kwaliteit van loquatfruit met methyljasmonaat:een onderzoek naar het suikermetabolisme en de dynamiek van genexpressie
- Waarom zou besnijdenis het risico van een man om AIDS op te lopen verminderen?
- Nakomelingen die identiek zijn aan hun ouders gebeld?
- Wat is een unieke eigenschap van stamcellen die ze?
- Onderzoek naar zeevogels aan de westkust laat zien hoe ze op een dag de lucht zouden kunnen delen met windturbines
- Wie is verantwoordelijk voor het dubbele helixmodel?
- Wat is Clostridium anthracis?
- Nieuwe studie vergroot het begrip van hoe antibioticaresistentie ontstaat
- De gevaarlijkste gebieden voor aanvaringen met schepen met walvishaaien onthuld
- De mechanische eigenschappen van spermastaarten onthuld
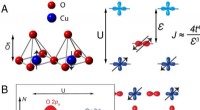
- Vreemde elektronen breken de kristalsymmetrie van supergeleiders bij hoge temperatuur

- Het gedrag van water - wetenschappers vinden nieuwe eigenschappen van H2O

- Belangrijke vooruitgang in natuurkundig onderzoek kan helpen om superefficiënte elektrische energie mogelijk te maken
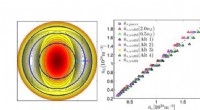
- Hogere plasmadichtheden, efficiëntere tokamaks
 Hoe zou u een monster van calcareniet onderscheiden van moddersteen met fossiele schelpen?
Hoe zou u een monster van calcareniet onderscheiden van moddersteen met fossiele schelpen?  Scores dood als recordbrekende hittegolf Canada in zijn greep houdt, ons
Scores dood als recordbrekende hittegolf Canada in zijn greep houdt, ons Welke relaties gebruikten om het procentuele opbrengst van een chemische reactie te bepalen?
Welke relaties gebruikten om het procentuele opbrengst van een chemische reactie te bepalen?  De Rode Zee is theoretiseerd als de locatie van een recent gevormde?
De Rode Zee is theoretiseerd als de locatie van een recent gevormde?  Hoe het Noorden
Hoe het Noorden  Gedigitaliseerde gezichten verminderen het risico op winkeldiefstal bij zelfbedieningskassa's
Gedigitaliseerde gezichten verminderen het risico op winkeldiefstal bij zelfbedieningskassa's Wat als een hoofdwatervoorziening besmet zou zijn met een of andere vorm van bacteriën?
Wat als een hoofdwatervoorziening besmet zou zijn met een of andere vorm van bacteriën?  Een hydraulische lift maken voor een schoolproject
Een hydraulische lift maken voor een schoolproject
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

