
Wetenschap
Een benadering voor het construeren van niet-Hermitische topologische invarianten in de reële ruimte
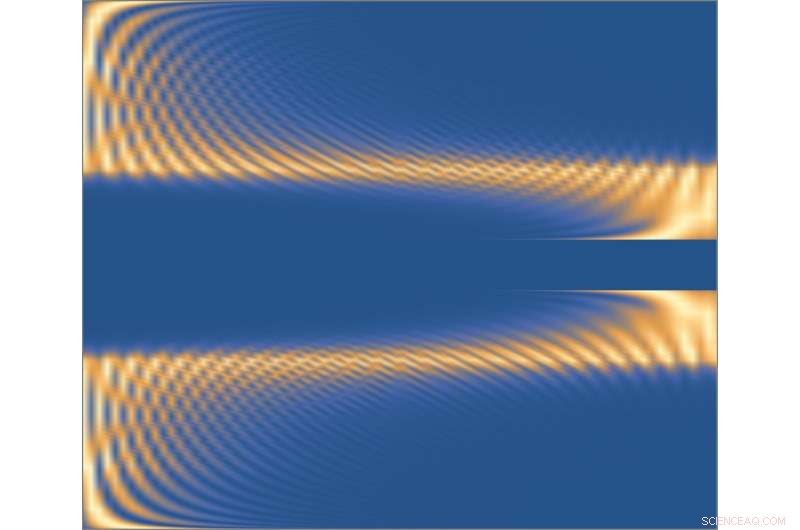
Een figuur die het ‘bipolaire niet-Hermitiaanse huideffect’ laat zien. De door de onderzoekers bedachte benadering van topologische invarianten is ook bij aanwezigheid van dit effect eenvoudig toe te passen. Krediet:Lied, Yao &Wang.
in de natuurkunde, niet-Hermitische systemen zijn systemen die niet standaard kunnen worden beschreven (d.w.z. Hermitische) wetten van de kwantummechanica, of meer precies, dat kan alleen worden beschreven door niet-Hermitiaanse Hamiltonianen. Niet-Hermitische systemen zijn alomtegenwoordig van aard. Veel open systemen, d.w.z., systemen die niet volledig geïsoleerd zijn van de rest van de wereld, behoren tot deze klasse. De topologie van deze systemen (d.w.z. robuuste eigenschappen die immuun zijn voor elke verandering van parameters) wordt fundamenteel gevormd door het zogenaamde "niet-Hermitiaanse huideffect, " wat leidt tot onconventionele bulk-grenscorrespondentie, die nooit is waargenomen in Hermitische systemen.
Het principe van bulk-grenscorrespondentie creëert in wezen een relatie tussen een bulkeigenschap van een materiaal dat is gecodeerd in een topologische invariant en wat er aan de grens ervan gebeurt (bijv. op het oppervlak of de randen). Om deze bulk-grenscorrespondentie te formuleren, natuurkundigen hebben een algemene en berekenbare definitie van topologische invarianten nodig.
Tot dusver, de meeste constructies van niet-Hermitische topologische invarianten zijn gebaseerd op een mooi geometrisch object dat bekend staat als de gegeneraliseerde Brillouin-zone (GBZ), die vorig jaar voor het eerst werd geïntroduceerd door een team van onderzoekers van de Tsinghua University in China. Deze berekening, echter, kan soms erg moeilijk zijn om uit te voeren (bijv. voor ongeordende systemen), vooral voor minder ervaren wetenschappers.
Om deze beperking te overwinnen, dezelfde onderzoekers die de GBZ-berekening presenteerden, kwamen onlangs met een eenvoudigere en gebruiksvriendelijkere constructie van topologische invarianten. Ze presenteerden deze nieuwe aanpak in een paper gepubliceerd in Fysieke beoordelingsbrieven .
"We kiezen voor een real-space golffunctiebenadering, die werd gestimuleerd door eerdere studies naar Hermitische systemen door Alexei Kitaev en daaropvolgende werken van anderen, "Zhong Wang, een van de onderzoekers die het onderzoek heeft uitgevoerd, vertelde Phys.org. "Op het eerste gezicht, deze real-space benadering lijkt ongeschikt voor niet-Hermitische systemen vanwege het eigenaardige gedrag dat bekend staat als het "niet-Hermitische huideffect" van niet-Hermitische systemen. Maar op een gegeven moment, we realiseerden ons dat het zelfs zou kunnen werken in de aanwezigheid van een niet-Hermitiaans huideffect. Inderdaad, het doet."
De nieuwe benadering voor het berekenen van topologische invarianten, voorgesteld door Wang en zijn collega's, omvat eerst de berekening van de golffuncties van een systeem in de reële ruimte, wat een standaardprocedure is. Zodra deze golffuncties zijn berekend, de niet-Hermitische topologische invarianten kunnen eenvoudig worden berekend met behulp van een reeks formules die door de onderzoekers zijn geïntroduceerd.
Een belangrijk kenmerk van deze nieuwe constructie die door de onderzoekers wordt voorgesteld, is dat het de zogenaamde 'open-grensconditie' vereist. In feite, de periodieke randvoorwaarde, die over het algemeen wordt gebruikt bij het bestuderen van Hermitische systemen, tot ongeldige resultaten zou leiden.
"Onze studie biedt een eenvoudige benadering voor niet-Hermitische topologische invarianten, en verdiept ook ons begrip van de niet-Hermitische topologie, " zei Wang. "Deze aanpak heeft verschillende voordelen. Eerst, het is gebruiksvriendelijk; tweede, het is breed toepasbaar (bijv. het kan worden toegepast op willekeurige systemen waarin de gegeneraliseerde Brillouin-zone niet gemakkelijk te definiëren is)."
De eenvoudige en intuïtieve benadering die door Wang en zijn collega's werd geïntroduceerd, zou enig licht kunnen werpen op enkele van de meest verwarrende aspecten van niet-Hermitische topologie en niet-Bloch-bandtheorie. Hun constructie levert ook overtuigend bewijs dat bepaalde eigenaardige en toch algemene kenmerken van niet-Hermitische systemen zijn, in feite, waar en natuurlijk.
In de toekomst, de theorie zou een aantal toepassingen in de echte wereld kunnen hebben. Bijvoorbeeld, het zou kunnen helpen bij het ontwerpen van hoogwaardige lasers op basis van topologische ideeën.
"We werken nu samen met experimentele natuurkundigen om meer niet-Hermitische opvattingen tot werkelijkheid te brengen, Wang zei. "Onder andere inspanningen, we onderzoeken de rijke veellichamenfysica van niet-Hermitische systemen, die momenteel slecht wordt begrepen."
© 2019 Wetenschap X Netwerk
 Voorbeelden van adsorptie
Voorbeelden van adsorptie  Onderzoekers rapporteren nieuwe toestand van materie beschreven als vloeibaar glas
Onderzoekers rapporteren nieuwe toestand van materie beschreven als vloeibaar glas Eiwitbatterijen produceren voor veiligere, milieuvriendelijke energieopslag
Eiwitbatterijen produceren voor veiligere, milieuvriendelijke energieopslag Wetenschapsexperimenten met betrekking tot de kinetische moleculaire gassentheorie
Wetenschapsexperimenten met betrekking tot de kinetische moleculaire gassentheorie Elektronische grensvlaktoestand die de waterstofopslagcapaciteit in Pd-MOF-materialen verbetert
Elektronische grensvlaktoestand die de waterstofopslagcapaciteit in Pd-MOF-materialen verbetert
Hoofdlijnen
- Hoe fotosynthese licht vangt en het leven op aarde aandrijft
- Wat onderscheidt mensen van chimpansees en andere apen?
- Iraakse dierenliefhebbers gaan online om zwerfdieren in Bagdad te redden
- Lijst van forensische technieken
- Hoe isoleer ik bacteriën uit de bodem?
- Twee nieuwe soorten schaaldieren ontdekt op Galicische zeebodem
- Windparken langs bergruggen kunnen vleermuizen negatief beïnvloeden
- Een reisbrochure van Science Cell maken
- Verschil tussen gekoppelde en vrijstaande ribosomen
- Een nieuwe licht-spin-interface met europium(III)-molecuul bevordert de ontwikkeling van kwantumcomputers
- Hybride apparaat oogst zowel mechanische als magnetische energie

- Atoomschakelaars door plasmonische verwarming van metalen contactpunten

- Onderzoek onthult de spontane polarisatie van nieuwe ultradunne materialen
- Wanneer uw röntgenonderwerp vleugels heeft - in insecten turen met de geavanceerde fotonbron

 New Yorks Central Park wordt officieel autovrij
New Yorks Central Park wordt officieel autovrij Betere manier gevonden om de integriteit van metalen te bepalen
Betere manier gevonden om de integriteit van metalen te bepalen Hoe een kristal wordt opgelost in water
Hoe een kristal wordt opgelost in water Ontleden van colloïdale glazen met laser als lancet
Ontleden van colloïdale glazen met laser als lancet Het recept voor sterrenhopen:Neem een gaswolk met een diameter van 500 lichtjaar, voeg 5 miljoen jaar toe, proces voor een maand
Het recept voor sterrenhopen:Neem een gaswolk met een diameter van 500 lichtjaar, voeg 5 miljoen jaar toe, proces voor een maand Wat is de CO2-voetafdruk van een plastic fles?
Wat is de CO2-voetafdruk van een plastic fles?  Uber voegt 2 toe, 000 banen in Chicago, meestal in Vrachteenheid:
Uber voegt 2 toe, 000 banen in Chicago, meestal in Vrachteenheid: Hoe bouw je een draaiend Jenny Paper Model
Hoe bouw je een draaiend Jenny Paper Model
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Portuguese | Swedish | German | Dutch | Danish | Norway | Spanish |

-
Wetenschap © https://nl.scienceaq.com

