
Wetenschap
Wat is de afstand tussen 2 puntenwetenschap?
1. Geometrie:
* Euclidische afstand: De meest voorkomende manier om afstand te berekenen, het gebruikt de stelling van Pythagoras om de rechte afstand tussen twee punten in een vlak of ruimte te vinden.
* Manhattan -afstand: Ook bekend als taxicab -afstand, berekent het de afstand door de absolute verschillen van hun coördinaten op te tellen. Dit is handig voor situaties waarin beweging beperkt is tot een raster, zoals stadsblokken.
* Great-cirkel afstand: Gebruikt voor het berekenen van afstanden op een bol, zoals het aardoppervlak. Het gebruikt de booglengte van de grote cirkel die door de twee punten gaat.
2. Fysica:
* verplaatsing: De rechte afstand en richting van de beginpositie naar de uiteindelijke positie van een object. Het is een vectorhoeveelheid.
* afgelegde afstand: De totale lengte van het pad dat door een object is genomen. Het is een scalaire hoeveelheid.
3. Astronomie:
* parallax: Het meten van de afstand tot sterren door hun schijnbare verschuiving in positie te observeren tegen een achtergrond van meer verre sterren.
* lichtjaren: Een afstandseenheid die wordt gebruikt om astronomische afstanden te meten, die de afstand vertegenwoordigen die licht in één jaar reist.
4. Computerwetenschappen:
* Afstandsmetrieken: Gebruikt om de gelijkenis of ongelijkheid tussen gegevenspunten in machine learning en gegevensanalyse te meten. Voorbeelden zijn Euclidische afstand, Manhattan -afstand en cosinus gelijkenis.
hoe afstand te berekenen:
De specifieke formule die wordt gebruikt om afstand te berekenen, hangt af van de context en de geometrie van het probleem. Hier zijn enkele voorbeelden:
* Euclidische afstand in twee dimensies:
√ ((x2 - x1) ² + (y2 - y1) ²)
* Euclidische afstand in drie dimensies:
√ ((x2 - x1) ² + (y2 - y1) ² + (z2 - z1) ²)
* Manhattan -afstand:
| x2 - x1 | + | y2 - y1 |
Naast de formules zijn er verschillende tools en software die u kunnen helpen de afstand te berekenen, zoals online rekenmachines, GIS -software en programmeerbibliotheken.
Uiteindelijk is het begrijpen van het concept van afstand essentieel voor het oplossen van problemen in verschillende wetenschappelijke disciplines. Het stelt ons in staat om ruimtelijke relaties te meten en te kwantificeren, waardoor het een belangrijk hulpmiddel is voor het analyseren en interpreteren van gegevens.
 Wat is de grootste bron van natuurlijk licht?
Wat is de grootste bron van natuurlijk licht?  Vulkaan Guatemala barst uit, maar nog geen evacuaties
Vulkaan Guatemala barst uit, maar nog geen evacuaties Boek beschrijft vier belangrijke facetten van de Green New Deal en waarom ze werkelijkheid kunnen worden
Boek beschrijft vier belangrijke facetten van de Green New Deal en waarom ze werkelijkheid kunnen worden Wat is er ter wereld die je ziet, maar het kan ruiken?
Wat is er ter wereld die je ziet, maar het kan ruiken?  NASA ziet Iris de Zombie Storm herboren in de buurt van Queensland
NASA ziet Iris de Zombie Storm herboren in de buurt van Queensland
Hoofdlijnen
- Nieuwe inzichten in hoe het HIV-1 envelopeiwit assembleert en opneemt
- Hoe worden ecosystemen en biomen verbonden?
- Nieuwe technologie verandert de manier waarop eiwitten in individuele cellen worden bestudeerd
- Hoe kent u wetenschappelijk onderzoek bij dieren en mensen?
- Zijn alle organismen hetzelfde in de eerste fase van ontwikkeling?
- Is Leucocyten kleurloos deel in je lichaam?
- Wat is het proces door welke organismen energie verkrijgen en vrijgeven?
- Is fytoplankton een gewervelde of ongewervelde dieren?
- Wat zijn drie belangrijkste delen van de celtheorie?
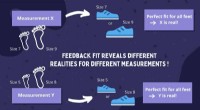
- Experimentele demonstratie van meetafhankelijke realiteiten mogelijk, onderzoeker zegt:
- Nieuwe microscoop en ionenversneller van GBP 3,5 miljoen nu operationeel

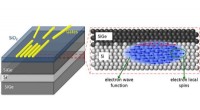
- Silicium biedt middelen om kwantumbits te besturen voor snellere algoritmen
- Universele optothermische micro/nanoschaal rotoren

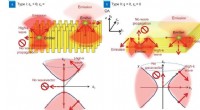
- Fotoluminescentiecontrole door hyperbolische metamaterialen en meta-oppervlakken
 Welke ionen worden gebruikt in natriumhydroxide?
Welke ionen worden gebruikt in natriumhydroxide?  Waar kan chroom mee combineren?
Waar kan chroom mee combineren?  De geest heeft de geest van de maan overgenomen:hoe Torres Strait Islanders verduisteringen voorspellen
De geest heeft de geest van de maan overgenomen:hoe Torres Strait Islanders verduisteringen voorspellen  Draadloze wereld:wat vrouwen willen
Draadloze wereld:wat vrouwen willen  Pool spelen met atomen
Pool spelen met atomen Een nieuwe act voor opera
Een nieuwe act voor opera Grafeen biedt bescherming tegen intense laserpulsen
Grafeen biedt bescherming tegen intense laserpulsen Wat gebeurt er met de kracht als de afstand tussen 2 objecten kleiner wordt?
Wat gebeurt er met de kracht als de afstand tussen 2 objecten kleiner wordt?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap & Ontdekkingen © https://nl.scienceaq.com

