
Wetenschap
Zou de matrixmechanica vandaag de dag erkenning krijgen?
Hier is een perspectief op hoe matrixmechanica vandaag de dag zou kunnen worden ontvangen, gezien de vooruitgang en het begrip dat sinds de introductie in de kwantumfysica is verworven:
1. Aanvankelijk scepticisme: De matrixmechanica zou, zoals elke revolutionaire theorie, waarschijnlijk ook in de huidige wetenschappelijke gemeenschap op aanvankelijk scepticisme stuiten. Het radicale vertrek van klassieke concepten en het wiskundig formalisme zou vragen kunnen oproepen over de geldigheid en bruikbaarheid ervan.
2. Theoretische ondersteuning: De afgelopen eeuw heeft de kwantumtheorie een uitgebreide ontwikkeling ondergaan, met talloze experimentele bevestigingen en wiskundige bewijzen. De matrixmechanica is nu stevig verankerd in de kwantummechanica als een van de fundamentele formuleringen ervan, naast de golfmechanica. De wiskundige elegantie en consistentie ervan met andere kwantumtheorieën zouden de geloofwaardigheid ervan versterken.
3. Computationele kracht: Moderne computertechnologie en vooruitgang in numerieke methoden hebben het gemakkelijker gemaakt om complexe matrixbewerkingen uit te voeren. Dit zou helpen bij de praktische implementatie en simulatie van kwantumsystemen, waardoor het nut en de betekenis van matrixmechanica verder zou worden ondersteund.
4. Pedagogische waarde: Matrixmechanica wordt nog steeds beschouwd als een belangrijk pedagogisch hulpmiddel bij het onderwijzen van de kwantumtheorie op universitair niveau. De nadruk op lineaire operatoren en matrixrepresentaties biedt een rigoureuze en intuïtieve manier om kwantumfenomenen te begrijpen, als aanvulling op op golffuncties gebaseerde benaderingen.
5. Interdisciplinaire toepassingen: Matrixmechanica heeft toepassingen gevonden in verschillende disciplines buiten de natuurkunde, waaronder scheikunde, informatica en techniek. Het vermogen om kwantumsystemen in verschillende contexten te modelleren vergroot de relevantie en erkenning ervan op deze terreinen.
6. Historische context: De huidige wetenschappelijke gemeenschap is ontvankelijker voor nieuwe en onconventionele ideeën vergeleken met het begin van de 20e eeuw. De lessen die zijn geleerd uit de historische ontwikkeling van de kwantumtheorie zouden een open geest en de bereidheid om alternatieve formuleringen te verkennen aanmoedigen.
Concluderend:hoewel er aanvankelijk enkele bedenkingen zijn vanwege de abstracte wiskundige aard ervan, zou de matrixmechanica waarschijnlijk erkenning krijgen in het huidige wetenschappelijke landschap vanwege de theoretische onderbouwing, de computationele bruikbaarheid, de pedagogische waarde, de interdisciplinaire toepassingen en de historische betekenis ervan binnen het bredere veld van de wetenschap. kwantumfysica.
 Door licht geactiveerde metaalkatalysator vernietigt vitale energiebron van kankercellen
Door licht geactiveerde metaalkatalysator vernietigt vitale energiebron van kankercellen Hoe 'plakkerig' is dichte nucleaire materie?
Hoe 'plakkerig' is dichte nucleaire materie?  Nuttige microben inhaleren koolstofdioxide via een poreuze cilindrische elektrode en scheiden nuttige chemicaliën uit
Nuttige microben inhaleren koolstofdioxide via een poreuze cilindrische elektrode en scheiden nuttige chemicaliën uit Niet langer haren over atomen splitsen?
Niet langer haren over atomen splitsen?  Onderzoekers ontwikkelen microscoop om lichtenergiestroom in fotosynthetische cellen te volgen
Onderzoekers ontwikkelen microscoop om lichtenergiestroom in fotosynthetische cellen te volgen
Hoofdlijnen
- Zou de ontdekking van een sleutelgensysteem de laatste zucht van koralen kunnen verstikken?
- Zijn genen ons lot? 'Verborgen' code in DNA evolueert sneller dan genetische code, ontdekken wetenschappers
- Zoete compromissen:het ontrafelen van de genetische puzzel van aardbeiensmaak en -opbrengst
- Hoewel de lucht vol stikstof zit, kunnen organismen deze niet gemakkelijk gebruiken. In welke stoffen veranderde stikstof voordat het door levende wezens werd gebruikt?
- Onderzoeken hoe overspraak tussen organellen de groei van bacteriën in macrofagen beperkt
- De functies van de linker temporale kwab
- Hoe zijn hypothese en experiment met elkaar verbonden?
- Wat is het element van S en O?
- Hoe worden eiwitten in de cel gesorteerd? Onderzoeksteam lost deze tien jaar oude puzzel op
- Schaalbare fotonische computer lost het deelverzamelingsomprobleem op

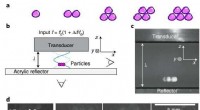
- Assemblage in de lucht:geluid gebruiken om de zwaartekracht te trotseren
- Kijken met radiogolven

- Veelbelovende nieuwe techniek brengt de microscopische details van de hersenen scherper in beeld

- Natuurkundigen creëren 's werelds kleinste motor

 Een exotische metaal-isolator overgang in een aan het oppervlak gedoteerd overgangsmetaal dichalcogenide
Een exotische metaal-isolator overgang in een aan het oppervlak gedoteerd overgangsmetaal dichalcogenide Wetenschappers introduceren kosmochemisch model voor Pluto-vorming
Wetenschappers introduceren kosmochemisch model voor Pluto-vorming De lege plekken invullen:hoe supercomputers röntgenbeelden met hoge resolutie kunnen ondersteunen
De lege plekken invullen:hoe supercomputers röntgenbeelden met hoge resolutie kunnen ondersteunen  De herfstnachten in Tampa worden heter:waarom onderzoekers zich zorgen maken
De herfstnachten in Tampa worden heter:waarom onderzoekers zich zorgen maken  Uit onderzoek blijkt dat u krijgt waar u voor betaalt met online vraag- en antwoordsites
Uit onderzoek blijkt dat u krijgt waar u voor betaalt met online vraag- en antwoordsites  Wat is het verschil tussen zeoliet en diatomeeënaarde?
Wat is het verschil tussen zeoliet en diatomeeënaarde?  Kleine schedels wijzen op menselijke migratiesnelweg naar Australië
Kleine schedels wijzen op menselijke migratiesnelweg naar Australië Matchmaking met gevolgen
Matchmaking met gevolgen
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

