
Wetenschap
Twee wiskundigen leggen uit hoe het bouwen van bruggen binnen het vakgebied heeft bijgedragen aan het bewijzen van de laatste stelling van Fermat
Toen ik aan de reis begon om de laatste stelling van Fermat te bewijzen, was samenwerking essentieel. Het zou een onmogelijke opgave zijn geweest om dit alleen aan te pakken, en ik had het geluk omringd te zijn door enkele van de meest briljante geesten in het veld.
Eerst en vooral ben ik veel dank verschuldigd aan mijn onderzoeksadviseur, Ken Ribet. Het was Ribets baanbrekende werk op het gebied van elliptische krommen en modulaire vormen dat de weg vrijmaakte voor de aanpak die ik uiteindelijk gebruikte. Zijn inzichten en begeleiding waren van fundamenteel belang bij het vormgeven van mijn onderzoeksrichting.
Daarnaast had ik het voorrecht om samen te werken met gerenommeerde experts op verschillende wiskundige deelgebieden. Nick Katz leverde waardevolle expertise op het gebied van p-adische analyse en rekenkundige meetkunde. Barry Mazur bood diepgaande inzichten in de verbanden tussen modulaire vormen en getaltheorie. Het werk van Henri Darmon over elliptische krommen en Galois-representaties speelde een cruciale rol in mijn bewijs.
Elk van deze samenwerkingen verrijkte mijn begrip en bracht nieuwe perspectieven op de uitdagingen die voor mij lagen. We brachten vaak uren door met het bespreken van ideeën, het uitwisselen van concepten en het verfijnen van onze aanpak. Het was een echte intellectuele onderneming die de individuele bijdragen te boven ging.
Het was inspirerend om te zien hoe de collectieve expertise van de wiskundige gemeenschap samenkwam voor een gemeenschappelijk doel. Het bewijs van de Laatste Stelling van Fermat toonde de kracht van interdisciplinaire samenwerking aan en versterkte onze overtuiging dat door collectieve inspanning zelfs ogenschijnlijk hardnekkige problemen kunnen worden overwonnen.
Richard Taylor:
Andrew, het bewijs van de Laatste Stelling van Fermat was een voorbeeld van de geest van samenwerking en de diepgaande impact van het bouwen van bruggen binnen onze discipline. Mijn betrokkenheid concentreerde zich op het vermoeden van modulariteit, dat een centraal onderdeel van het bewijs vormde.
Samen met Andrew kwamen we talloze obstakels tegen die de inbreng van experts uit verschillende domeinen vereisten. Eén van die uitdagingen was het construeren van bepaalde modulaire vormen. Om dit te ondervangen hebben we de expertise van Michael Harris en Bill Casselman ingeroepen. Hun kennis van representatietheorie en automorfe vormen stelde ons in staat doorbraken te realiseren op dit cruciale aspect.
Bovendien was het verkrijgen van een dieper inzicht in elliptische krommen over functievelden cruciaal. In dit streven hebben we samengewerkt met Gerd Faltings en Chandrashekhar Khare, gerenommeerde experts op het gebied van de algebraïsche meetkunde. Dankzij hun inzichten konden we onze aanpak verfijnen en specifieke technische problemen aanpakken die zich voordeden.
Toen het bewijs van de stelling zijn voltooiing naderde, stonden we voor de uitdaging om de rekenkunde van elliptische krommen en modulaire vormen met elkaar te verbinden. Dit vereiste dat we ons moesten verdiepen in de ingewikkelde wereld van Galois-representaties. Samenwerking met specialisten als Jean-Pierre Serre en Christopher Skinner was van cruciaal belang bij het tot stand brengen van de noodzakelijke verbindingen en het bevestigen van de laatste stappen van het bewijs.
De succesvolle samenwerking tussen zoveel wiskundigen uit diverse vakgebieden demonstreerde de onderlinge verbondenheid van de wiskunde en het belang van het voeden van verschillende onderzoekslijnen. Zonder de bereidheid van onderzoekers om ideeën uit te wisselen, constructieve feedback te geven en hun expertise in te zetten, zou het bewijs van Fermats laatste stelling misschien ongrijpbaar zijn gebleven.
Over het geheel genomen leidde de geest van samenwerking die onze onderzoeksinspanningen doordrenkte niet alleen tot een significante wiskundige doorbraak, maar bevorderde het ook een gevoel van kameraadschap onder wiskundigen over de hele wereld, wat de collectieve kracht van onze discipline demonstreerde om zelfs de meest formidabele uitdagingen aan te pakken.
 Lang gehypothetiseerd wondermateriaal van de volgende generatie voor het eerst gemaakt
Lang gehypothetiseerd wondermateriaal van de volgende generatie voor het eerst gemaakt Wetenschappers elimineren bijwerkingen van medicijnen door moleculaire chiraliteit te manipuleren
Wetenschappers elimineren bijwerkingen van medicijnen door moleculaire chiraliteit te manipuleren Gemodificeerde bacterie zet aardolie direct om in bouwstenen voor kunststoffen
Gemodificeerde bacterie zet aardolie direct om in bouwstenen voor kunststoffen Beheersing van vitamine K2-productie in de tuberculosebacterie
Beheersing van vitamine K2-productie in de tuberculosebacterie Hoe een badspons een biobased industrieel filter wordt
Hoe een badspons een biobased industrieel filter wordt
 Studiedetails bewijs voor eerdere grote aardbevingen in de seismische zone van Oost-Tennessee
Studiedetails bewijs voor eerdere grote aardbevingen in de seismische zone van Oost-Tennessee Hoe een Nederlandse man die zwerfvuil verzamelde in een wetenschappelijk artikel belandde
Hoe een Nederlandse man die zwerfvuil verzamelde in een wetenschappelijk artikel belandde Natuurlijk archief onthult Atlantische stormen door de tijd heen
Natuurlijk archief onthult Atlantische stormen door de tijd heen Lessen van Parkfield helpen bij het voorspellen van aanhoudende breukbewegingen na aardbevingen
Lessen van Parkfield helpen bij het voorspellen van aanhoudende breukbewegingen na aardbevingen Metingen voor kardinaal Birdhouses
Metingen voor kardinaal Birdhouses
Hoofdlijnen
- Wat wetenschappers weten over de glans van de juweelkever
- Introns versus Exons: Wat zijn de overeenkomsten & verschillen?
- Zal op cel gebaseerde melk de zuivelindustrie veranderen? Dit laboratorium in Californië kan het voortouw nemen
- Welke genen en genomen onthullen over onze gezondheid
- Onderzoekers ontdekken dat een klein organisme de kracht heeft om een hardnekkig broeikasgas op landbouwvelden te verminderen
- Opnieuw nadenken over hoe cellen reageren op stress
- De opkomst van microbiële valsspelers in ijzerarme omgevingen:onderzoek onthult hun evolutionaire geschiedenis
- Epigenetische inzichten:hoe hybride populier scheuten regenereert
- Genetische studie onthult seksgeheimen van schimmels werpt licht op candidiasis
- On-chip lichtbron produceert een veelzijdig bereik aan golflengten

- Nieuwe benadering van exotische kwantummaterie
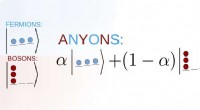
- Machtige morphing materialen nemen complexe vormen aan

- Natuurkundigen onthullen hoe beweging kan worden gegenereerd door frustratie

- Plasmawetenschappers optimaliseren plantengroei en opbrengst

 Nieuwe inzichten in het toxine achter tetanus
Nieuwe inzichten in het toxine achter tetanus Samenwerken als een virtuele telescoop, observatoria over de hele wereld produceren de eerste directe beelden van een zwart gat
Samenwerken als een virtuele telescoop, observatoria over de hele wereld produceren de eerste directe beelden van een zwart gat Eenvoudige experimenten met chemische verandering voor 4de sorteermachines
Eenvoudige experimenten met chemische verandering voor 4de sorteermachines  Creëer een WTO-equivalent om toezicht te houden op internet, beveelt nieuw rapport aan
Creëer een WTO-equivalent om toezicht te houden op internet, beveelt nieuw rapport aan Hoe SETI werkt
Hoe SETI werkt  Waarom uitzoeken hoe kalium in sterren wordt vernietigd belangrijk is voor het begrijpen van het universum
Waarom uitzoeken hoe kalium in sterren wordt vernietigd belangrijk is voor het begrijpen van het universum  Onderzoekers gebruiken hete nano-beitel om kunstmatige botten in een petrischaal te maken
Onderzoekers gebruiken hete nano-beitel om kunstmatige botten in een petrischaal te maken Welke vaardigheden heeft een cybersecurityprofessional nodig?
Welke vaardigheden heeft een cybersecurityprofessional nodig?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

