
Wetenschap
Ontwerpen van Dirac vortex topologische fotonische kristalvezels
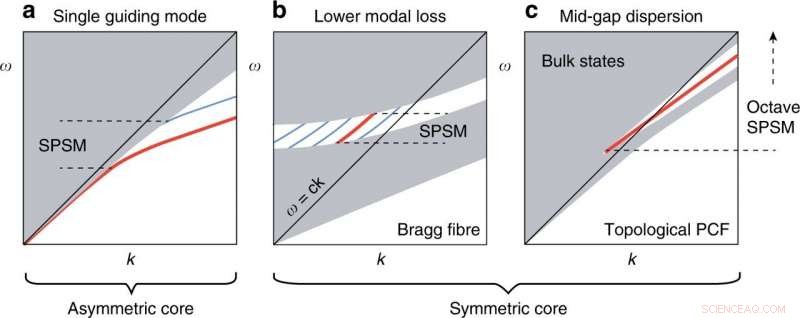
Asymmetrische en symmetrische benaderingen van een SPSM. (a) Dominante benadering om de gedegenereerde fundamentele modi te splitsen door structurele asymmetrie. (b) Voorgesteld Bragg-vezelontwerp om licht te geleiden door een enkelvoudig gedegenereerde modus met minder verlies dan andere modi. (c) De topologische PCF biedt singlet mid-gap-dispersie voor een breedband-SPSM. Credit:Licht:Wetenschap &Toepassingen, doi:10.1038/s41377-020-00432-2
Optische vezels gemaakt van topologische fotonische kristallen zorgen voor een verbeterde veelzijdigheid en controle over de modi en polarisatie van het licht dat ze doorlaten. compositie, fotonische kristallen bevatten bandgaps om de doorgang van licht ten opzichte van specifieke golfenergieën en momenta te voorkomen, net als een aan/uit-schakelaar. In een nieuw rapport dat nu is gepubliceerd op Natuurlicht:wetenschap en toepassingen , Ha Lin, en Ling Lu van het Institute of Physics van de Chinese Academie van Wetenschappen zond puur "single mode" licht uit over een groot frequentiebereik via een topologisch kenmerk dat bekend staat als een "Dirac-vortex". Het concept kan leiden tot toepassingen die lichtsignalen stabieler over lange afstanden verzenden. Hoewel het werk momenteel theoretisch is, de onderzoekers suggereren het gebruik van vezels gemaakt van silica op basis van stapel-en-trekmethoden of driedimensionale (3D) printtechnologieën om deze theoretische concepten te fabriceren en te testen.
De knooplijnen en Weyl-punten in een fotonische kristalvezel begrijpen.
Fotonische kristalvezels vertrouwen voor hun functionaliteit op de eindeloze verscheidenheid aan tweedimensionale (2-D) kristallen. Het concept van topologische fotonica op basis van robuuste golfgeleiders kan inspireren tot nieuwe vezelconcepten, waaronder de ontwikkeling van een eenrichtingsvezel in een magnetische, 3D fotonisch kristal. In dit werk, Lin en Lu introduceerden een topologische fotonische kristalvezel (PCF) die lijkt op de topologische holte van de Dirac-vortex in zijn dwarsdoorsnede met behulp van 2D-fotonische kristallen. De Dirac vortexvezel is een ideaal ontwerp om ultrabreedband single-polarization single-mode (SPSM) vezels te ontwikkelen vanwege de singlet mid-gap dispersie binnen de bandgap. De wetenschappers vergemakkelijkten de fabricagestap door een vereenvoudigd ontwerp van slechts vier capillaire silicabuizen te introduceren om uiteindelijk een octaaf-overspannende SPSM te bereiken.
Het team begon met de meest voorkomende fotonische kristalvezel, een fotonisch kristal van silica met een driehoekig rooster van luchtgaten. Het materiaal bevatte twee knooplijnen van 2D Dirac-punten in de Brillouin-zone. Als ze de inversiesymmetrie van de fotonische kristalvezel hebben verbroken door een extra klein luchtgat in de primitieve cel toe te voegen, elke knooplijn van het construct zou kunnen gapen in Weyl-punten of topologische ladingen op het materiaal. Weyldeeltjes zijn ongrijpbare fermionische deeltjes met verdwijnende massa en komen in de natuur niet voor als elementair deeltje. Ze worden in plaats daarvan gevonden in vastestofmaterialen waar 3D-banden een topologisch beschermde puntachtige kruising kunnen ontwikkelen, bekend als een Weylpunt. Fotonische Weyl-punten kunnen worden gerealiseerd in 3D-fotonische kristallen met complexe structuren.
Banddiagram van silica (ε = 2.1) fotonische kristalroosters uniform in de richting buiten het vlak (z). (a) Geprojecteerd banddiagram van het driehoekige fotonische kristal, waarin de degeneratie van de knooplijn wordt benadrukt. (b) Een extra luchtgat in de primitieve cel verbreekt de inversiesymmetrie, en de knooplijn wordt opgetild in Weylpunten. Inzetstukken:dwarsdoorsnedestructuren en bandstructuren in het vlak bij kza/2π = 2.02. Twee verschillende primitieve celkeuzes zijn getekend in (a). Credit:Licht:Wetenschap &Toepassingen, doi:10.1038/s41377-020-00432-2 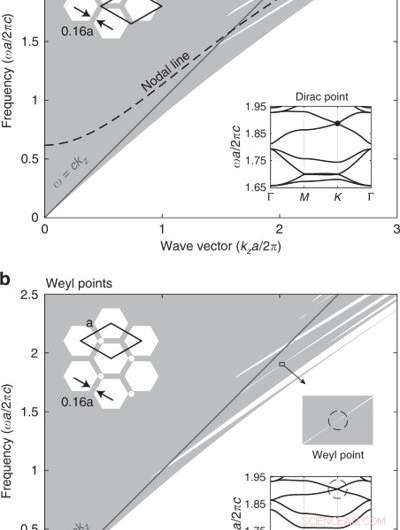
De topologische gebonden toestand die in dit werk wordt onderzocht, kan ook worden gerealiseerd in honingraatroosters met afwisselende enkele en dubbele bindingsrepresentaties van organische verbindingen die bekend staan als Kekulé-structuren, vernoemd naar de Duitse chemicus August Kekulé, die oorspronkelijk de voorstelling voorstelde om de organische benzeenverbinding te ontwikkelen. De onderzoekers koppelden vervolgens de twee knooplijnen van Dirac-punten in een vergrote supercel en vernietigden ze in een bandgap. Elke supercel had drie primitieve cellen gelabeld als een kunstmatig 'atoom' met drie stutten. Ze verplaatsten elk atoom in de structuur door het zwaartepunt in elke richting te verschuiven door de dikte van de drie stutten aan te passen zonder de totale massa van het atoom te veranderen. De wetenschappers ontwikkelden Kekulé-modulaties van de roosters en tekenden hun corresponderende bandstructuur.
De stabiliteit van de Dirac vortex fotonische kristalvezel bleef in het ontwerp zelf, aangezien het overeenkomstige topologische defect niet werd gevormd door lokaal materiaal toe te voegen of te verwijderen. Het topologische defect werd gevormd door het hele rooster voorzichtig te verstoren om kleine lokale onvolkomenheden te creëren. Een bepalend topologisch kenmerk van de Dirac-vortexvezel was het gemak van het creëren van meerdere bijna gedegenereerde modi door het opwindgetal te verhogen - d.w.z. een geheel getal dat het aantal keren vertegenwoordigt dat krommen tegen de klok in rond een punt gaan, van de draaikolk. In principe, kunnen de onderzoekers praktisch een continue, single-mode of multimode Dirac vortex fotonische kristalvezel, hetzij van 3D-geprinte preforms (een vorm of vorm), of via de stack-and-draw-methode die wordt gebruikt om optische vezels te ontwikkelen met meer dan honderd buizen met verschillende buisdiktes. Echter, geen van deze methoden was handig, daarom Lin en Lu et al. presenteerde een discrete versie van vezelontwerp.
Dirac-vortexvezel verkregen door continue Kekulé-modulaties. (a) Voorbeeld van hoe een "atoom" in elke richting kan worden verschoven (arg[δ] = ϕ) met eindige amplitude (|δ|) door de breedte van de drie stutten te veranderen. (b1), (c1), (d1) Supercell-voorbeelden van drie gecoördineerde atomen (A1, A2, en A3). De corresponderende bandstructuren zijn uitgezet in (b2), (c2), en (d2), respectievelijk. (e) Structuur van een continue Dirac-vortex PCF, waarin elke stut is gekleurd volgens zijn breedte. (f) Banddiagram van de vezel uitgezet met verwijzing naar de frequentie van de oorspronkelijke knooplijn (centrale stippellijn). De inzet toont de intensiteitspatronen van de topologische modus en één lokale defectmodus. De topologische modus met enkele polarisatie (rode lijn) beslaat meer dan twee octaven. Credit:Licht:Wetenschap &Toepassingen, doi:10.1038/s41377-020-00432-2 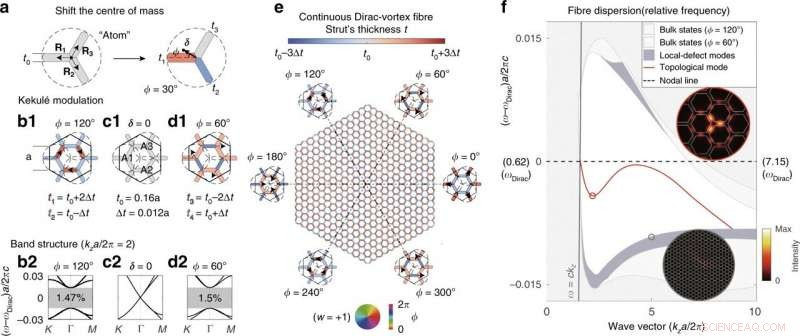
De onderzoekers hadden slechts vier buizen nodig om de Dirac vortex fotonische kristalvezel te stapelen en te tekenen, wat zeer redelijk was voor fabricage. De vier silicabuizen die in het proces werden gebruikt, hadden dezelfde buitendiameter om het rooster te behouden, maar verschillende binnendiameters voor modulatie. De onderzoekers plotten de resulterende discrete Dirac-vortexvezel en de gebonden structuur waarin structurele niet-uniformiteit aanwezig was op zes identieke interfaces. Ze merkten ook de aanwezigheid op van indexgeleide modi in de Dirac-vortexvezel die optraden waar een scherp lokaal maximum van de stutdikte aanwezig was. Deze kwamen overeen met een lokale stijging van de effectieve brekingsindex. De wetenschappers noteerden ook de vezeldoorsnede met de vortexgrootte en de bijbehorende bandstructuur.
De Dirac vortex fotonische kristalvezel met een eindige vortexdiameter handhaafde een single-polarization single-mode (SPSM). Lin en Lu et al. hun potentiële prestaties getest ten opzichte van het opsluitingsverlies, verspreiding en effectief gebied en buigend verlies. Ze zetten de modi uit met het laagste opsluitingsverlies en merkten op dat het verlies van de topologische modus de laagste was voor het hele golflengtebereik over een octaaf. De specificaties van de Dirac vortex fotonische kristalvezel die hier worden beschreven, waren vergelijkbaar met die in eerdere studies, hoewel met het belangrijkste verschil van een enkele polarisatiemodus, gebruikt in dit werk.
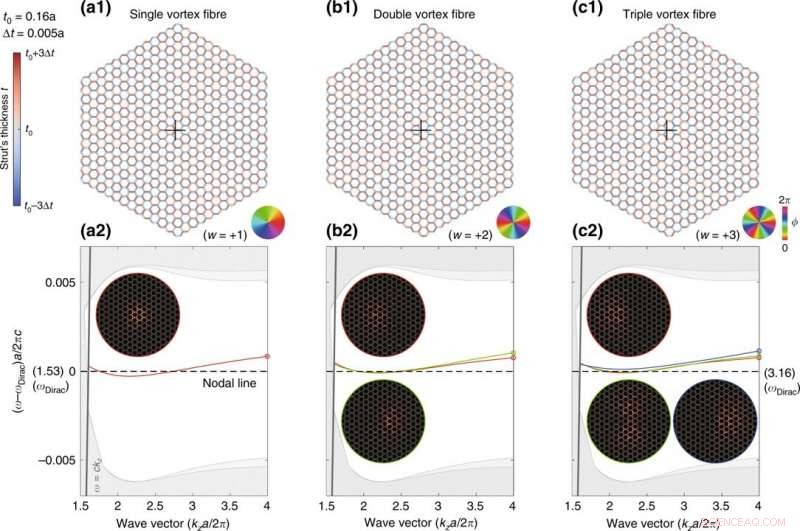
Continue Dirac-vortexvezels met wikkelnummer w = +1, +2, +3. (a1), (b1), en (c1) zijn de vezelstructuren. De kleurenwielen tonen de overeenkomstige fasen van de gegeneraliseerde Kekulé-modulatie. (a2), (b2), en (c2) zijn de corresponderende banddiagrammen, en de inzetstukken tonen de modusprofielen (zˆ⋅Re[E∗×H]) van modi bij kza/2π = 4. Credit:Light:Science &Applications, doi:10.1038/s41377-020-00432-2
Octave SPSM in een continue Dirac-vortex-vezel met een eindige vortex-grootte. (a) Vezelstructuur met 16 bekledingsperioden in straal. Het kleurenwiel vertegenwoordigt de fase en amplitude van de gegeneraliseerde Kekulé-modulatie. (b) Volledige vezeldispersie in absolute frequentie. Eerste topologische modus (rode lijn) en doubletmodi van hogere orde (groene stippellijn) in de eerste topologische bandgap, evenals een tweede topologische modus (blauwe lijn) in de tweede topologische bandgap bij hogere frequentie. De modusprofielen (zˆ⋅Re[E∗×H]) van de twee topologische modi worden weergegeven in de inzetstukken, voor de duidelijkheid omcirkeld met verschillende kleuren. (c) Vezeldispersie in frequentie ten opzichte van de oorspronkelijke knooplijnfrequentie. (d) Opsluitingsverliezen van de geleide modi. (e) Dispersieparameter en effectief gebied van de eerste topologische modus. (f) Buigverlies van de eerste topologische modus bij λ = 1550 nm. Credit:Licht:Wetenschap &Toepassingen, doi:10.1038/s41377-020-00432-2 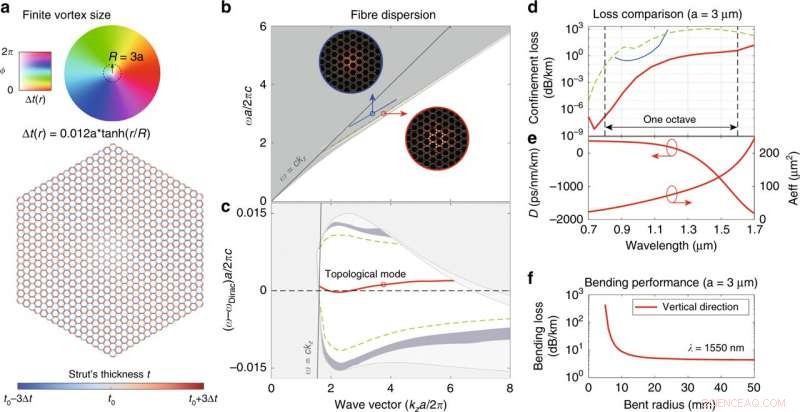
Op deze manier, Hao Lin en Ling Lu onderzochten numeriek de Dirac vortex topologische fotonische kristalvezel ten opzichte van zijn principe, constructie en potentiële prestaties. Ze stelden voor om deze vezel te ontwikkelen met behulp van het standaard stapel-en-trekproces met behulp van silicaglazen buizen of 3D-geprinte preforms. De methode is voordelig in vergelijking met eerdere vezels vanwege het vermogen om een willekeurig aantal bijna gedegenereerde modi naar believen te begeleiden. Het single-mode ontwerp zorgde voor de single-polarisatie, single-mode vezel met een octaafbandbreedte om het effectieve modusgebied gemakkelijk af te stemmen door de vortexgrootte in het materiaal te veranderen. Het werk suggereert het gebruik van fotonische kristalvezels als een nieuw platform voor topologische fotonica.
© 2020 Wetenschap X Netwerk
 Nieuwe watersplitsingskatalysator kan het gemakkelijker maken om zonnebrandstof te genereren
Nieuwe watersplitsingskatalysator kan het gemakkelijker maken om zonnebrandstof te genereren Plastic
Plastic Nieuw kathodemateriaal voor hoogwaardige natriumionbatterijen zou kunnen profiteren van grootschalige energieopslag
Nieuw kathodemateriaal voor hoogwaardige natriumionbatterijen zou kunnen profiteren van grootschalige energieopslag Elektrolytboost verbetert de prestaties van waterige dual-ion-batterijen
Elektrolytboost verbetert de prestaties van waterige dual-ion-batterijen Fladderende vleugels aangedreven door de zon
Fladderende vleugels aangedreven door de zon
Hoofdlijnen
- Hier is hoe planten- en dierencellen verschillen
- 7 soorten bindweefsel
- Een 3D-poster maken van de celcyclus
- Wisseling van de wacht - onderzoek werpt licht op hoe planten ademen
- Dierentuin Praag viert gezondheid zeldzame Maleise tijgerwelpen
- 10 oudst bekende ziekten
- DNA versus RNA: wat zijn de overeenkomsten en verschillen? (met diagram)
- Wat is een regeling in de microbiologie?
- Makeup Science Projects
- Zeldzame supergeleider kan van vitaal belang zijn voor quantum computing

- Neutronenproductie bij ORNLs SNS bereikt ontwerpvermogensniveau

- Onderzoekers tonen aan dat silicium fysieke fenomenen kan reproduceren die worden uitgebuit door geavanceerde telecommunicatieapparatuur

- Quantum dots visualiseren minuscule trillingsresonanties

- Hoe een hydraulische cilinder te bouwen

 Nieuw, gratis website helpt tieners, volwassenen met speciale behoeften maken nieuwe vrienden
Nieuw, gratis website helpt tieners, volwassenen met speciale behoeften maken nieuwe vrienden Hoe wordt warmte overgedragen van de zon naar de aarde?
Hoe wordt warmte overgedragen van de zon naar de aarde?  Laserkoeling van een nanomechanische oscillator dicht bij de grondtoestand
Laserkoeling van een nanomechanische oscillator dicht bij de grondtoestand Berekenen van uitvalpercentage
Berekenen van uitvalpercentage Nanodeeltjes bieden inzicht in interacties tussen enkelstrengs DNA en hun bindende eiwitten
Nanodeeltjes bieden inzicht in interacties tussen enkelstrengs DNA en hun bindende eiwitten Waarborgen van de veiligheid van offshore koolstofopslag
Waarborgen van de veiligheid van offshore koolstofopslag Canadese minister van klimaat dringt aan op vooruitgang akkoord Parijs
Canadese minister van klimaat dringt aan op vooruitgang akkoord Parijs Studie bevestigt dat oude Spaanse grotkunst is gemaakt door Neanderthalers
Studie bevestigt dat oude Spaanse grotkunst is gemaakt door Neanderthalers
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Swedish | German | Dutch | Norway | Portuguese | Danish |

-
Wetenschap © https://nl.scienceaq.com

