
Wetenschap
Hoe berekent u de grootte van de resulterende kracht in de fysica?
Inzicht in de resulterende kracht
* krachten: Krachten zijn duwt of trekt die ervoor kunnen zorgen dat een object versnelt (wijzig de snelheid of richting). Ze hebben zowel grootte (sterkte) als richting.
* resulterende kracht: De resulterende kracht is de enkele kracht die hetzelfde effect heeft als alle individuele krachten die op een object werken. Het is alsof je het netto -effect van alle gecombineerde krachten vindt.
methoden voor het berekenen van de resulterende kracht
1. Vector -toevoeging (grafische methode)
* Teken vectoren: Teken elke kracht als een pijl. De lengte van de pijl vertegenwoordigt de grootte en de richting van de pijl vertegenwoordigt de richting van de kracht.
* staart-to-heading: Plaats de staart van de tweede vector aan het hoofd van de eerste vector. Ga door dit voor alle krachten.
* resultant: Trek een vector uit de staart van de eerste vector naar de kop van de laatste vector. Dit is uw resulterende kracht.
* Meet: Meet de lengte van de resulterende vector om de grootte ervan te bepalen en de richting ten opzichte van een referentiepunt.
2. Vector -toevoeging (analytische methode)
* Breek in componenten: Los elke kracht op in zijn horizontale (x) en verticale (y) componenten met behulp van trigonometrie (sinus en cosinus).
* Sum -componenten: Voeg alle horizontale componenten bij elkaar toe om de totale horizontale component (RX) te krijgen. Doe hetzelfde voor de verticale componenten (RY).
* Pythagorische stelling: Zoek de grootte van de resulterende kracht met behulp van de Pythagorische stelling:r =√ (rx² + ry²)
* richting: Bepaal de richting van de resulterende kracht met behulp van de arctangent -functie:θ =tan⁻¹ (ry/rx)
Voorbeeld:twee krachten op rechtse hoeken
Laten we zeggen dat we twee krachten hebben:
* F1: 5 N (Newton) aan de rechterkant
* f2: 12 N omhoog
1. Grafische methode:
* Teken F1 horizontaal naar rechts, 5 eenheden lang.
* Teken F2 verticaal omhoog, 12 eenheden lang, beginnend bij het hoofd van F1.
* Teken de resulterende kracht R van de staart van F1 naar de kop van F2.
2. Analytische methode:
* componenten: F1x =5 n, f1y =0 n; F2x =0 n, f2y =12 n
* som: Rx =5 n, ry =12 n
* magnitude: R =√ (5² + 12²) =√ (169) =13 n
* richting: θ =tan⁻¹ (12/5) ≈ 67.38 ° (gemeten vanaf de horizontale, omhoog)
Key Points
* eenheden: Zorg ervoor dat alle krachten in dezelfde eenheden worden uitgedrukt (meestal Newton, N).
* richting: Overweeg altijd de richting van elke kracht.
* vectoren: Krachten zijn vectorhoeveelheden, wat betekent dat ze zowel grootte als richting hebben.
Laat het me weten als je meer specifieke voorbeelden wilt doorlopen of nog vragen wilt hebben!
 Wat is een afvalproduct van de ademhaling?
Wat is een afvalproduct van de ademhaling?  Leg uit waarom waterstof een ionische binding met fluor zal vormen, maar vormt alleen covalente bindingen koolstof?
Leg uit waarom waterstof een ionische binding met fluor zal vormen, maar vormt alleen covalente bindingen koolstof?  Poreuze enkelkristallijne monolieten op centimeterschaal met Lewis-zuurplaatsen met hoge dichtheid om propaandehydrogena te verbeteren
Poreuze enkelkristallijne monolieten op centimeterschaal met Lewis-zuurplaatsen met hoge dichtheid om propaandehydrogena te verbeteren Wat is een nauwkeurige vergelijking van het verbindings- en eigenschappenelement dat bevat?
Wat is een nauwkeurige vergelijking van het verbindings- en eigenschappenelement dat bevat?  Atomen die of elektronen in hun valentieschalen hebben, hebben de neiging om vormgeladen ionen te krijgen?
Atomen die of elektronen in hun valentieschalen hebben, hebben de neiging om vormgeladen ionen te krijgen?
 Is de consequentialistische ethiek belangrijk in het behoud en is het een essentiële componenten de biodiversiteit?
Is de consequentialistische ethiek belangrijk in het behoud en is het een essentiële componenten de biodiversiteit?  Wat zijn de oorzaken van gevaarlijk afval?
Wat zijn de oorzaken van gevaarlijk afval?  Welke uitspraken zijn waar over natuurlicht?
Welke uitspraken zijn waar over natuurlicht?  Het klimaatproject dat de manier veranderde waarop we extreem weer begrijpen
Het klimaatproject dat de manier veranderde waarop we extreem weer begrijpen  Waarom wordt de omgeving genaamd Environment?
Waarom wordt de omgeving genaamd Environment?
Hoofdlijnen
- Hoe ziet een menselijke cel eruit?
- Wat vormt een embryo?
- Welke organellen hebben de bacteriecel en de plant gemeen?
- Computers verklaren waarom peren bruin kunnen worden tijdens commerciële opslag
- Wat heeft een wetenschapper nodig om de wetenschappelijke vraag te beantwoorden?
- Spinnen of brullen sabeltandtijgers? Het antwoord ligt misschien in een klein stukje bot
- Hoe ras het luisteren tijdens politieke gesprekken beïnvloedt
- Heeft messenger-RNA een fosfaatgroep?
- Welke rol speelt stikstof om de continuïteit van het leven te waarborgen?
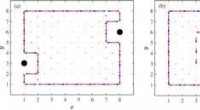
- Hoe weeg je een enkel molecuul?
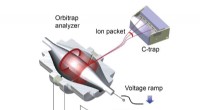
- Testen van Hawking-straling in laboratoriumanalogen van zwart gat

- Theoretische berekeningen voorspelden nu bevestigde tetraneutron, een exotische toestand van materie

- Uit hoeveel atomen bestaat een persoon?

- De randstromen die niet met de stroom meegaan:wetenschappers doen merkwaardige kwantumontdekking
 Is astrologisch symbool en astronomie hetzelfde?
Is astrologisch symbool en astronomie hetzelfde?  Hoe kunnen krachten op een object handelen zonder aan te raken?
Hoe kunnen krachten op een object handelen zonder aan te raken?  Wat zijn de verstoringen van de zon?
Wat zijn de verstoringen van de zon?  Wat is 30 nanoseconden in wetenschappelijke notatie?
Wat is 30 nanoseconden in wetenschappelijke notatie?  De Nederlandse kennis is mogelijk in massavernietigingswapens terechtgekomen
De Nederlandse kennis is mogelijk in massavernietigingswapens terechtgekomen  Zijn alle symbiotische organismen onschadelijk voor mensen?
Zijn alle symbiotische organismen onschadelijk voor mensen?  Wat voor soort golf wordt gemaakt als een boom in het bos valt?
Wat voor soort golf wordt gemaakt als een boom in het bos valt?  Reageert ijzer met geconcentreerd salpeterzuur?
Reageert ijzer met geconcentreerd salpeterzuur?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap © https://nl.scienceaq.com

