
Wetenschap
Als een basketbalspeler de bal van 2,0 m in de lucht naar de lucht 10 meter weg gooit, is 3,05 m uit de grond en de eerste hoek 40 graden welke snelheid?
1. Begrijp het probleem
We hebben een projectielbewegingsprobleem. Het basketbal wordt onder een hoek gelanceerd en we moeten de beginsnelheid vinden waardoor het de hoepel bereikt.
2. Definieer variabelen
* initiële hoogte (y 0 ): 2.0 m
* horizontale afstand (x): 10 m
* laatste hoogte (y): 3,05 m
* Starthoek (θ): 40 °
* Initiële snelheid (V 0 ): Dit is wat we moeten vinden.
* versnelling als gevolg van zwaartekracht (g): -9.8 m/s² (negatief omdat het naar beneden werkt)
3. Vergelijkingen instellen
We zullen de volgende bewegingsvergelijkingen gebruiken voor projectielbeweging:
* horizontale beweging: x =V 0x * T
* V 0x =V 0 * cos (θ)
* Verticale beweging: y =y 0 + v 0y * t + (1/2) * g * t²
* v 0y =V 0 * sin (θ)
4. Oplossen voor tijd (t)
* Vind de vluchttijd (t) met behulp van de horizontale bewegingsvergelijking:
* t =x / v 0x =x / (v 0 * cos (θ))
5. Vervang tijd in de verticale bewegingsvergelijking
* Vervang de uitdrukking voor 't' van stap 4 in de verticale bewegingsvergelijking:
* y =y 0 + v 0 * sin (θ) * (x / (v 0 * cos (θ))) + (1/2) * g * (x/(v 0 * cos (θ))) ²
* Vereenvoudig de vergelijking:
* y =y 0 + x * tan (θ) + (1/2) * g * (x²/(v 0 ² * cos² (θ))))
6. Los op voor de initiële snelheid (V 0 )
* herschik de vergelijking om op te lossen voor V 0 :
* V 0 ² =(g * x² / (2 * (y - y 0 - x * tan (θ)) * cos² (θ))))
* V 0 =√ (g * x² / (2 * (y - y 0 - x * tan (θ)) * cos² (θ))))
7. Sluit de waarden aan en bereken
* Vervang de bekende waarden in de vergelijking:
* V 0 =√ (9,8 m / s² * (10 m) ² / (2 * (3,05 m - 2,0 m - 10 m * tan (40 °)) * cos² (40 °)))
* Bereken de beginsnelheid:
* V 0 ≈ 11,6 m/s
Daarom moet de basketbalspeler de bal gooien met een beginsnelheid van ongeveer 11,6 m/s om de hoepel te bereiken.
 Hoe warmteoverdracht door geleiding?
Hoe warmteoverdracht door geleiding?  Onderzoek creëert waterstofproducerende levende druppeltjes, weg vrijmaken voor alternatieve toekomstige energiebron
Onderzoek creëert waterstofproducerende levende druppeltjes, weg vrijmaken voor alternatieve toekomstige energiebron Hoeveel therms in een MCF van aardgas?
Hoeveel therms in een MCF van aardgas?  Wat voor soort elementen zijn haliden oxiden sulfaten sulfiden carbonaten en natieve elementen?
Wat voor soort elementen zijn haliden oxiden sulfaten sulfiden carbonaten en natieve elementen?  Waarom worden elementen chemisch afgebroken?
Waarom worden elementen chemisch afgebroken?
 Onderzoek om zich te concentreren op hoe herten reageren op veranderingen in de maanfase en het weer
Onderzoek om zich te concentreren op hoe herten reageren op veranderingen in de maanfase en het weer  Plotselinge overstromingen, stormvloedwaarschuwing terwijl Isaias de oostkust van de VS binnenstormt
Plotselinge overstromingen, stormvloedwaarschuwing terwijl Isaias de oostkust van de VS binnenstormt Om verbonden te zijn met de natuur, kinderen hebben buiten eenzame activiteiten nodig
Om verbonden te zijn met de natuur, kinderen hebben buiten eenzame activiteiten nodig Plastic waait in de wind
Plastic waait in de wind Het ademhalingssysteem van een vlinder
Het ademhalingssysteem van een vlinder
Hoofdlijnen
- Wat is de rol van bacteriën binnen een voedselweb?
- Welke organel is verantwoordelijk voor het identificeren en verteren van beschadigde of gedenatureerde eiwitten?
- Welk fysiek kenmerk heeft de plantachtige Noctiluca en Animalle -Trypanosoma Gambienese gemeen?
- Gekruiste (evolutionaire) signalen?
- Wat doet een kern in mitose van enkele cel?
- Belang van diffusie in organismen
- Ben je zoals te wijten aan je genen of omgeving?
- Waarom lopen mensen meestal in dezelfde richting?
- Beschrijf het koppelingsgedrag van stikstofbases in DNA en RNA?
- Begin van de meest gevoelige zoektocht tot nu toe naar donkere materie axion

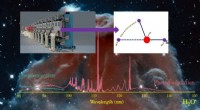
- Dalian Coherent Light Source onthult hydroxyl-superrotors uit waterfotochemie
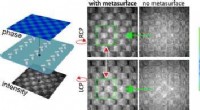
- Nieuwe nanotech imaging-tool maakt diagnose van smartphoneziekte mogelijk
- Kan een deeltjesversneller met behulp van lasergestuurde implosie werkelijkheid worden?

- Natuurkundigen demonstreren het bestaan van een nieuwe subatomaire structuur

 Nobelprijswinnende laserontdekkingen die het veld verlichtten
Nobelprijswinnende laserontdekkingen die het veld verlichtten Wat is de formule voor momentum gelijk aan de massa -snelheid van de massa?
Wat is de formule voor momentum gelijk aan de massa -snelheid van de massa?  Wat zijn deposito's gevormd wanneer door de wind opgeblazen sedimenten zich vestigen en zich ophopen achter een obstakel?
Wat zijn deposito's gevormd wanneer door de wind opgeblazen sedimenten zich vestigen en zich ophopen achter een obstakel?  Rook op het water -- en in de microfoon?
Rook op het water -- en in de microfoon?  De verschillende soorten leisteen rock?
De verschillende soorten leisteen rock?  Verbetering van de toediening van nanotherapeutische vaccins
Verbetering van de toediening van nanotherapeutische vaccins  Wat is een niet -contactkracht die wordt gecreëerd door de beweging van een elektrische lading?
Wat is een niet -contactkracht die wordt gecreëerd door de beweging van een elektrische lading?  Wat is de energietransformatie voor een zonnepaneel?
Wat is de energietransformatie voor een zonnepaneel?
- Elektronica
- Biologie
- Zonsverduistering
- Wiskunde
- French | Italian | Spanish | Portuguese | Swedish | German | Dutch | Danish | Norway |

-
Wetenschap & Ontdekkingen © https://nl.scienceaq.com

